微信网页上的网站怎么做的一键免费生成网页的网站
题目链接:https://leetcode.cn/problems/shu-ju-liu-zhong-de-zhong-wei-shu-lcof
1. 题目介绍(41. 数据流中的中位数)
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
- void addNum(int num) - 从数据流中添加一个整数到数据结构中。
- double findMedian() - 返回目前所有元素的中位数。
【测试用例】:
示例 1:
输入:
[“MedianFinder”,“addNum”,“addNum”,“findMedian”,“addNum”,“findMedian”]
[[],[1],[2],[],[3],[]]
输出:[null,null,null,1.50000,null,2.00000]
示例 2:
输入:
[“MedianFinder”,“addNum”,“findMedian”,“addNum”,“findMedian”]
[[],[2],[],[3],[]]
输出:[null,null,2.00000,null,2.50000]
【条件约束】:
限制:
- 最多会对 addNum、findMedian 进行 50000 次调用。
【相关题目】:
注意:本题与主站 295. 数据流的中位数 题目相同。
2. 题解
2.1 最大堆和最小堆(原书题解) – O(logn)
时间复杂度O(logn),空间复杂度O(n)
偶数情况:
【解题思路】:
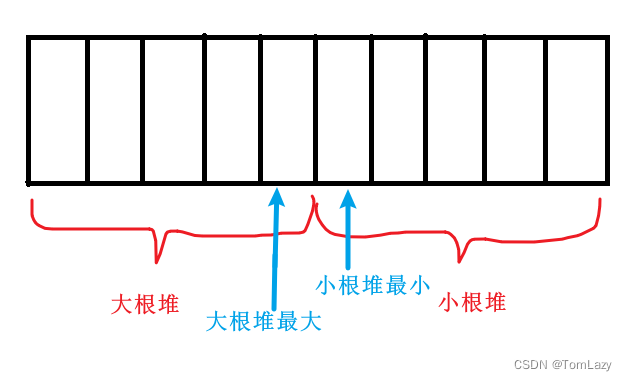
该题的解法很多,可以通过数组、链表、二叉搜索树、AVL树、最大堆和最小堆来实现,目前最推荐的就是使用最大堆和最小堆来解决该问题。该题可以将整个数据容器分成两部分,左边部分的数据要比右边的数据小。我们可以用一个最大堆实现左边的数据容器,用一个最小堆实现右边的数据容器。
两个保证:
- 要保证数据平均分配到两个堆中,两个堆中数据的数目之差不能超过1;
- 要保证最小堆中的所有数据都要大于最大堆中的数据
……
【实现策略】:
- 使用优先队列
PriorityQueue实现最大堆和最小堆,优先队列的底层实现是一个最小堆,通过重写比较器的方法,可以将其改为大根堆;
更多内容可参考:堆的实现(Java)- 分配数据的插入位置,如果数据的总数目是
偶数,则把新数据插入到小根堆,否则则插入到大根堆;- 保证堆中数据正确,即小根堆中所有数据都要大于大根堆中的数据,因此就要进行判断,如果出现了要插入小根堆中的数据小于大根堆中的数据的情况,那么则将该数据插入到大根堆,并将大根堆的队首元素(最大值)弹出插入到小根堆中;
- 返回中点时进行判断,如果总数是偶数,则返回中点两数的平均值,如果是奇数,则返回小根堆的最小值。
……
【注意点】:
==运算符的优先级要大于&运算符:
因此,在判断总数目是偶数时要注意加上括号:((minHeap.size() + maxHeap.size()) & 1) == 0,挺麻烦的就是说,但如果你不加括号,就会出现下列问题:
更多内容可参考:Java运算符优先级
class MedianFinder {// 最小堆 PriorityQueue<Integer> minHeap;// 最大堆PriorityQueue<Integer> maxHeap;/** initialize your data structure here. */public MedianFinder() {minHeap = new PriorityQueue<>();maxHeap = new PriorityQueue<>((i1, i2) -> Integer.compare(i2, i1));}public void addNum(int num) {// 如果总数目是偶数,则将数据存到小根堆if (((minHeap.size() + maxHeap.size()) & 1) == 0){if (maxHeap.size() > 0 && num < maxHeap.peek()){maxHeap.offer(num);minHeap.offer(maxHeap.poll());}else minHeap.offer(num);} else{ // 否则存到大根堆if (minHeap.size() > 0 && minHeap.peek() < num){minHeap.offer(num); maxHeap.offer(minHeap.poll()); }else maxHeap.offer(num);}}public double findMedian() {// 总数是偶数,返回两数平均值if (((minHeap.size() + maxHeap.size()) & 1) == 0){return (double)(minHeap.peek() + maxHeap.peek())/2;}else{ // 奇数,返回小根堆return minHeap.peek();}}
}/*** Your MedianFinder object will be instantiated and called as such:* MedianFinder obj = new MedianFinder();* obj.addNum(num);* double param_2 = obj.findMedian();*/
代码简化:
【简化思路】:
思路与上面差不多,只不过是简化省略了一些判断过程,直接将判断的过程扔给了堆,如:我要向大根堆插入一个数据,那么我就先要插入的数据扔到小根堆中,然后我把小根堆中最小的数插入大根堆,反之亦然,这样始终能保持小根堆存储较大一半、大根堆存储较小一半。
class MedianFinder {Queue<Integer> A, B;public MedianFinder() {A = new PriorityQueue<>(); // 小顶堆,保存较大的一半B = new PriorityQueue<>((x, y) -> (y - x)); // 大顶堆,保存较小的一半}public void addNum(int num) {if(A.size() != B.size()) {A.add(num);B.add(A.poll());} else {B.add(num);A.add(B.poll());}}public double findMedian() {return A.size() != B.size() ? A.peek() : (A.peek() + B.peek()) / 2.0;}
}

3. 参考资料
[1] 面试题41. 数据流中的中位数(优先队列 / 堆,清晰图解)