---

目录

一、平衡二叉树的介绍

二、平衡二叉树的插入

1、平衡二叉树的插入步骤

2、平衡二叉树的旋转

2.1左单旋

2.2右单旋

2.3左右双旋

2.4右左双旋

三、平衡二叉树的删除（略）

四、个人对平衡二叉树见解

五、平衡二叉树整体代码

---

一、平衡二叉树的介绍

二叉搜索树的目的是为了提高查找效率，但如果数据有序或者接近有序，那么二叉搜索树将会变成单支树，查找元素的效率等效为顺序表，树形结构的优势荡然无存。

为了解决这一问题，苏联数学家G.M.Adelson-Velskii和E.M.Landis便发明了平衡二叉树（AVL树）。

平衡二叉树：在一棵搜索二叉树中每个节点的左右子树的高度差的绝对值不超过1。左右子树的高度差被称为平衡因子（平衡因子=右子树高度-左子树高度）。若一颗平衡二叉树的节点个数为n，那么其高度为logN。

二、平衡二叉树的插入

1、平衡二叉树的插入步骤

平衡二叉树的插入第一步和二叉搜索树一样，根据二叉搜索树的特性，找到新插入节点位于整棵树的位置。

随后使用逻辑语句判断新节点是插入在父节点的左还是右，并维护其与父节点的指针关系。

新增在右，平衡因子++；新增在左，平衡因子--。那新插入了一个节点，原先的平衡二叉树的结构可能会遭到破坏，所以需要观察平衡因子的三种情况，进行分类讨论：如图

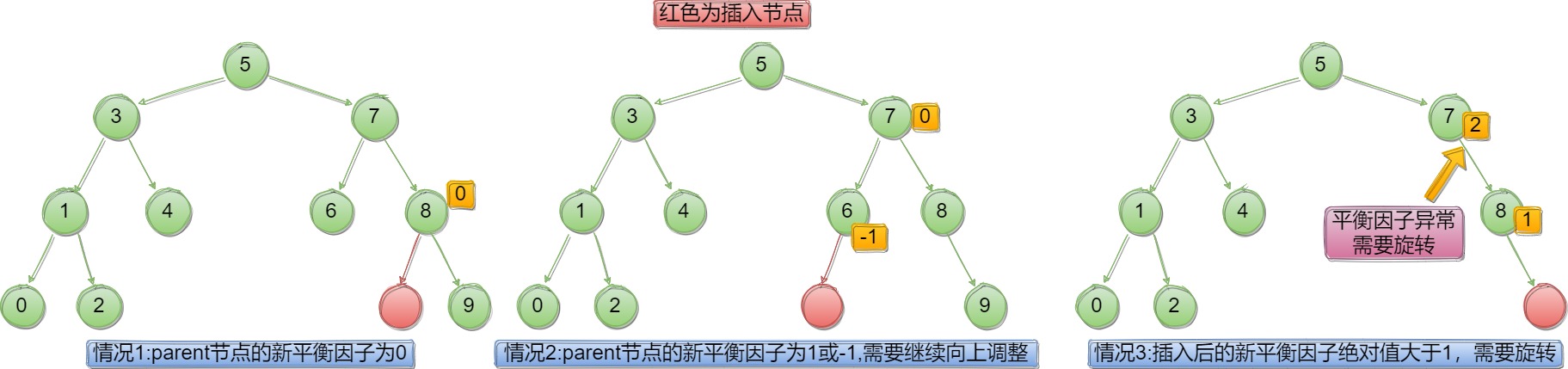
情况三如何旋转？无非是四种情况：

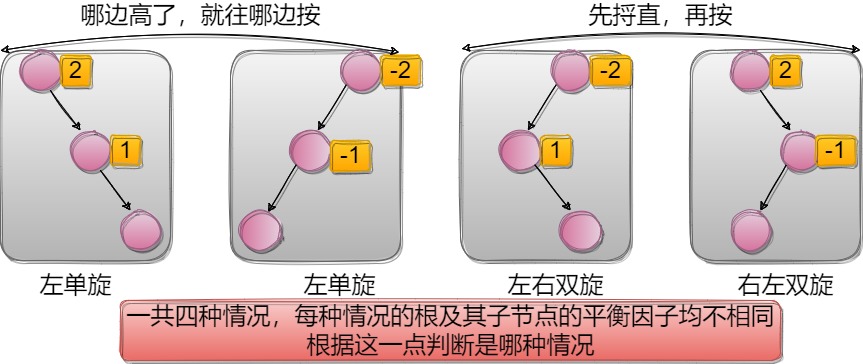
2、平衡二叉树的旋转

当出现上图情况三时，就需要对平衡二叉树的节点进行旋转，旋转的目的是要让这颗树继续维持平衡二叉树的形态，同时调节子树的高度，让其和插入前的高度保持一致，旋转后不要忘记更新那些被旋转的节点的平衡因子。

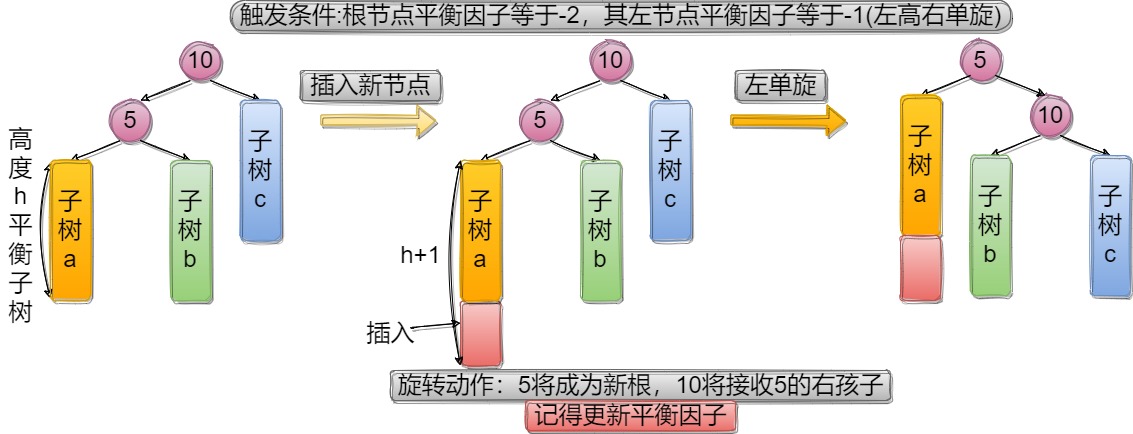
2.1左单旋

5可能是根，也可能是某颗子树的根，分类讨论：

void RotateLeft(Node* parent)//左单旋
{Node* grandfather = parent->_parent;Node* cur = parent->_right;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (grandfather->_left == parent)//需要判定parent原来属于grandfather的哪一边grandfather->_left = cur;elsegrandfather->_right = cur;cur->_parent = grandfather;}parent->_right = cur->_left;if (cur->_left != nullptr)cur->_left->_parent = parent;cur->_left = parent;parent->_parent = cur;//更新平衡因子cur->_bf = parent->_bf = 0;
}

2.2右单旋

void RotateRight(Node* parent)//右单旋
{Node* grandfather = parent->_parent;Node* cur = parent->_left;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (grandfather->_left == parent){grandfather->_left = cur;cur->_parent = grandfather;}else{grandfather->_right = cur;cur->_parent = grandfather;}}parent->_parent = cur;parent->_left = cur->_right;if (cur->_right != nullptr)cur->_right->_parent = parent;cur->_right = parent;//更新平衡因子cur->_bf = parent->_bf = 0;
}

2.3左右双旋

void RotateLR(Node* parent)//左右双旋
{Node* cur = parent->_left;Node* curR = cur->_right;int bf = curR->_bf;RotateLeft(parent->_left);RotateRight(parent);if (bf == -1)//curR的左树插入新节点{cur->_bf = 0;parent->_bf = 1;curR->_bf = 0;}else if (bf == 1)//curR的右树插入新节点{cur->_bf = -1;parent->_bf = 0;curR->_bf = 0;}else if (bf == 0)//curR自身为新增节点{cur->_bf = 0;parent->_bf = 0;curR->_bf = 0;}elseassert(false);//不可能出现这种情况
}

2.4右左双旋

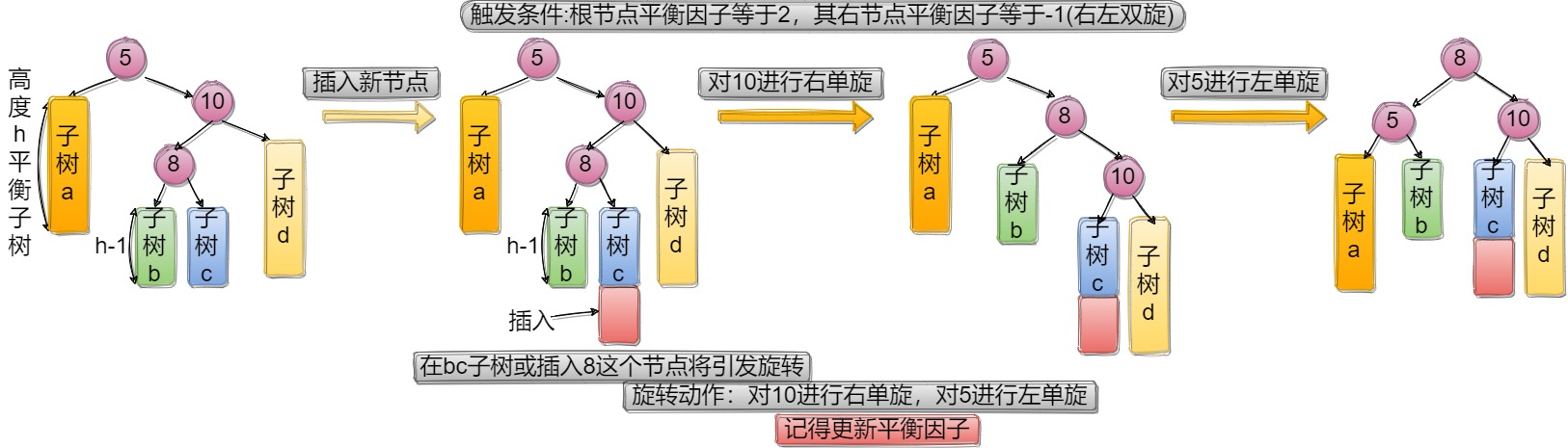
void RotateRL(Node* parent)//右左双旋
{Node* cur = parent->_right;Node* curL = cur->_left;int bf = curL->_bf;RotateRight(parent->_right);RotateLeft(parent);if (bf == -1)//curL的左树插入新节点{cur->_bf = 1;parent->_bf = 0;curR->_bf = 0;}else if (bf == 1)//curL的右树插入新节点{cur->_bf = 0;parent->_bf = -1;curR->_bf = 0;}else if (bf == 0)//curL自身为新增节点{cur->_bf = 0;parent->_bf = 0;curR->_bf = 0;}elseassert(false);//不可能出现这种情况
}

三、平衡二叉树的删除（略）

按照二叉搜索树的方式对平衡二叉树节点进行删除。更新平衡因子时，平衡因子为1或-1便可以停止向上更新。当平衡因子绝对值大于1时，同样需要进行旋转解决。

四、个人对平衡二叉树见解

平衡二叉树强就强在通过大量的旋转控制整颗树任意一个节点的左右子树高度差不大于1，使树的结构近似完全二叉树，搜索效率为logN。

但偏偏是频繁的旋转，导致其插入删除的效率并不及红黑树，这也是红黑树成为树形容器的原因。

但是一颗树仅用来查找而不进行删除的话，用平衡二叉树还是很棒的。

五、平衡二叉树整体代码

#pragma once
#include <iostream>
#include <cassert>
#include <map>
#include <set>
#include <time.h>
using namespace std;template <class K, class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;//Balance factor平衡因子AVLTreeNode(const pair<K, V>& kv): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}
};template <class K, class V>
struct AVLTree
{typedef AVLTreeNode<K, V> Node;//记住不要把这个<K,V>漏了！！！
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}//_root不为空Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else//相等说明元素相同，插入失败return false;}//开始插入cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;//维护cur的父指针}else{parent->_left = cur;cur->_parent = parent;}//更新平衡因子while (parent)//最坏情况更新到根{if (cur == parent->_left){--parent->_bf;}else if (cur == parent->_right){++parent->_bf;}//平衡因子更新完毕后，分析三种情况if (parent->_bf == 0)//父节点的平衡因子为零说明已经平衡break;else if (parent->_bf == 1 || parent->_bf == -1)//一边高一边低{//需要继续向上对平衡因子进行调整cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2)//父节点的平衡因子为2或-2，不满足平衡二叉树规则{//需要旋转调整if (parent->_bf == 2 && cur->_bf == 1)//触发左单旋条件{RotateLeft(parent);//左单旋}else if (parent->_bf == -2 && cur->_bf == -1)//触发右单旋条件{RotateRight(parent);//右单旋}else if (parent->_bf == -2 && cur->_bf == 1)//触发左右双旋{RotateLR(parent);//左右双旋}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);//右左双旋}else{assert(false);}break;//必定平衡，跳出循环}else//防止出现代码错误导致平衡因子绝对值出现大于3的情况（正常情况不会发生这种现象）{assert(false);}}return true;}void RotateLeft(Node* parent)//左单旋{Node* grandfather = parent->_parent;Node* cur = parent->_right;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (grandfather->_left == parent)//需要判定parent原来属于grandfather的哪一边grandfather->_left = cur;elsegrandfather->_right = cur;cur->_parent = grandfather;}parent->_right = cur->_left;if (cur->_left != nullptr)cur->_left->_parent = parent;cur->_left = parent;parent->_parent = cur;//处理平衡因子cur->_bf = parent->_bf = 0;}void RotateRight(Node* parent)//右单旋{Node* grandfather = parent->_parent;Node* cur = parent->_left;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (grandfather->_left == parent){grandfather->_left = cur;cur->_parent = grandfather;}else{grandfather->_right = cur;cur->_parent = grandfather;}}parent->_parent = cur;parent->_left = cur->_right;if (cur->_right != nullptr)cur->_right->_parent = parent;cur->_right = parent;//更新平衡因子cur->_bf = parent->_bf = 0;}void RotateLR(Node* parent)//左右双旋{Node* cur = parent->_left;Node* curR = cur->_right;int bf = curR->_bf;RotateLeft(parent->_left);RotateRight(parent);if (bf == -1)//curR的左树插入新节点{cur->_bf = 0;parent->_bf = 1;curR->_bf = 0;}else if (bf == 1)//curR的右树插入新节点{cur->_bf = -1;parent->_bf = 0;curR->_bf = 0;}else if (bf == 0)//curR自身为新增节点{cur->_bf = 0;parent->_bf = 0;curR->_bf = 0;}elseassert(false);//不可能出现这种情况}void RotateRL(Node* parent)//右左双旋{Node* cur = parent->_right;Node* curL = cur->_left;int bf = curL->_bf;RotateRight(parent->_right);RotateLeft(parent);if (bf == -1)//curL的左树插入新节点{cur->_bf = 1;parent->_bf = 0;curL->_bf = 0;}else if (bf == 1)//curL的右树插入新节点{cur->_bf = 0;parent->_bf = -1;curL->_bf = 0;}else if (bf == 0)//curL自身为新增节点{cur->_bf = 0;parent->_bf = 0;curL->_bf = 0;}elseassert(false);//不可能出现这种情况}int TreeHight(Node* root){if (root == nullptr)return 0;int leftHight = TreeHight(root->_left);int rightHight = TreeHight(root->_right);return leftHight > rightHight ? leftHight + 1 : rightHight + 1;}void Inorder(){_Inorder(_root);}bool IsBalance(){return _IsBalance(_root);}
private:void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);}bool _IsBalance(Node* root){if (root == nullptr)return true;int leftHight = TreeHight(root->_left);int rightHight = TreeHight(root->_right);//检查平衡因子对不对if (rightHight - leftHight != root->_bf){cout << "平衡因子出现异常" << endl;return false;}//需要递归检查是否平衡return (leftHight - rightHight <= 1 && leftHight - rightHight >= -1)&& _IsBalance(root->_left) && _IsBalance(root->_right);}
private:Node* _root = nullptr;
};
//void TestAVLTree()
//{
//	//int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
//	//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
//	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
//	//int a[] = { 9,8,7,6,5,4,3,2,1};
//	AVLTree<int, int> t;
//	for (auto e : a)
//	{
//		t.Insert(make_pair(e, e));
//	}
//
//	t.Inorder();
//
//	cout << t.IsBalance() << endl;
//}
void TestAVLTree()
{srand((unsigned int)time(0));const size_t N = 1000000;AVLTree<int, int> t;for (size_t i = 0; i < N; ++i){size_t x = rand();t.Insert(make_pair(x, x));//cout << t.IsBalance() << endl;}t.Inorder();cout << t.IsBalance() << endl;
}