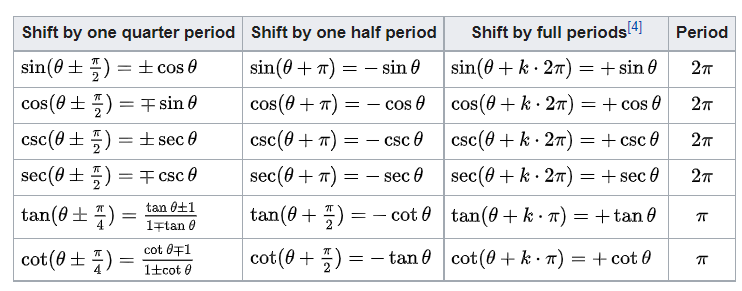老年门户网站建设的意义今日新闻网
文章目录
- 诱导公式
- 单位圆坐标和三角函数
- 记忆口诀
- 符号看象限
- 奇变偶不变
- 例
- 常用诱导公式🎈
- 常用部分(5对)
- 倒数关系
- 六种三角函数间的转换关系
- 小结
- Reflections
- Shifts and periodicity
诱导公式
- 诱导公式 - 维基百科,自由的百科全书 (wikipedia.org)
单位圆坐标和三角函数
-

-
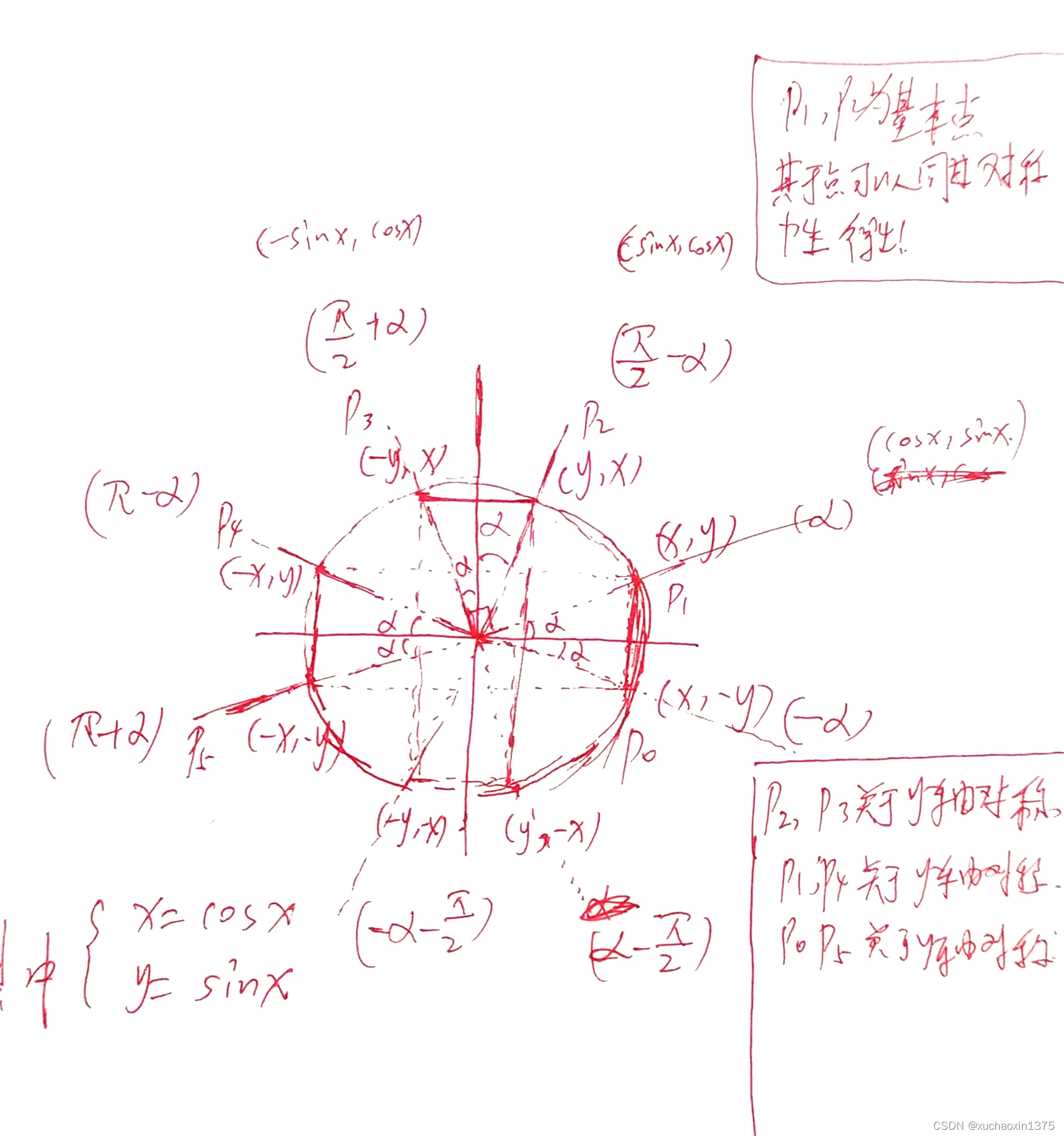
例如,sin(θ+π)=−sin(θ);这里ϕ(θ)=π+θsin(\theta+\pi)=- sin(\theta);这里\phi(\theta)=\pi+\thetasin(θ+π)=−sin(θ);这里ϕ(θ)=π+θ
-
途中各个点的横纵坐标分值分别对应p(cox(ϕ(θ)),sin(ϕ(θ)))途中各个点的横纵坐标分值分别对应p(cox(\phi(\theta)),sin(\phi(\theta)))途中各个点的横纵坐标分值分别对应p(cox(ϕ(θ)),sin(ϕ(θ)))
-
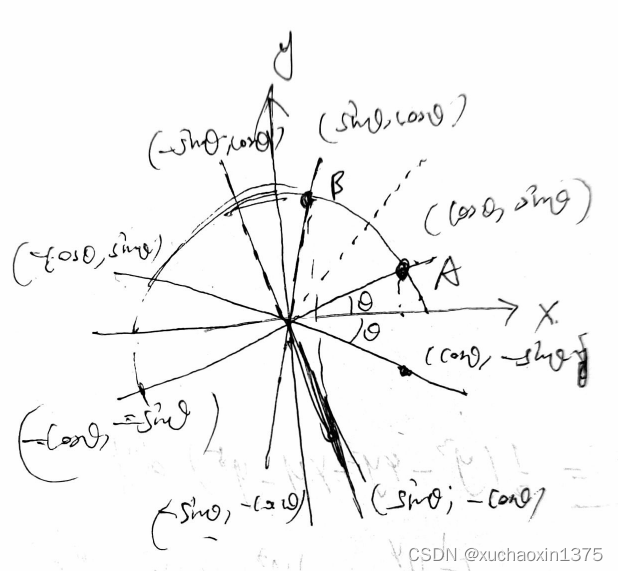
途中设定了两个超级点(主超级点为A(cosθ,sinθ),副超级点B(sinθ,cosθ)A(cos\theta,sin\theta),副超级点B(sin\theta,cos\theta)A(cosθ,sinθ),副超级点B(sinθ,cosθ)
- 所有的其他角度都可以由超级点关于x轴或者y轴或者圆心原点(或者θ=π2)对称所有的其他角度都可以由超级点关于x轴或者y轴或者圆心原点(或者\theta=\frac{\pi}{2})对称所有的其他角度都可以由超级点关于x轴或者y轴或者圆心原点(或者θ=2π)对称
- 比如ϕ(θ)=θ−π2;则sin(ϕ(θ))=−cosθ;cos(ϕ(θ))=sinθ\phi(\theta)=\theta-\frac{\pi}{2};则sin(\phi(\theta))=-cos\theta;cos(\phi(\theta))=sin\thetaϕ(θ)=θ−2π;则sin(ϕ(θ))=−cosθ;cos(ϕ(θ))=sinθ
记忆口诀
- 对于kπ2±α(k∈Z)k\frac{\pi}{2}\pm\alpha(k\in \mathbb{Z})k2π±α(k∈Z)的三角函数值,
符号看象限
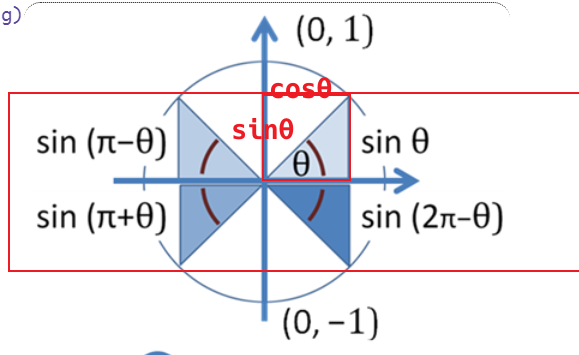
- 口诀总是把α\alphaα看作锐角,2π−α∈(270°,360°),弧度角2π−α终边落在第4象限,sin(2π−α)<02π-α∈(270°,360°),弧度角2\pi-\alpha终边落在第4象限,sin(2π-α)<02π−α∈(270°,360°),弧度角2π−α终边落在第4象限,sin(2π−α)<0,符号为“-”
奇变偶不变
-
当k是偶数时,得到α的同名函数值,即函数名不改变;
-
当k是奇数时,得到α相应的余函数值,即
- sin→cos;cos→sin;tan→cot,cot→tan
-
然后在前面加上把α看成锐角时原函数值的符号
-
对于tan,sec,csc,cot\tan,\sec,\csc,\cottan,sec,csc,cot可以转化为cos,sin\cos,\sincos,sin处理
例
- sin(2π−α)=sin(4⋅π2−α)sin(2π-α)=sin(4·\frac{\pi}{2}-α)sin(2π−α)=sin(4⋅2π−α),k=4为偶数,所以函数名(绝对值部分)是sinα\sin\alphasinα。
- 所以sin(2π−α)=−sinαsin(2π-α)=-sinαsin(2π−α)=−sinα
常用诱导公式🎈
常用部分(5对)
-
sin(−α)=−sinα\sin(-\alpha)=-\sin{\alpha}sin(−α)=−sinα
-
cos(−α)=cosα\cos(-\alpha)=\cos{\alpha}cos(−α)=cosα
-
sin(π2−α)=cosα\sin(\frac{\pi}{2}-\alpha)=\cos{\alpha}sin(2π−α)=cosα
-
cos(π2−α)=sinα\cos(\frac{\pi}{2}-\alpha)=\sin{\alpha}cos(2π−α)=sinα
-
sin(π2+α)=cosα\sin(\frac{\pi}{2}+\alpha)=\cos{\alpha}sin(2π+α)=cosα
-
cos(π2+α)=−sinα\cos(\frac{\pi}{2}+\alpha)=-\sin{\alpha}cos(2π+α)=−sinα
-
sin(π−α)=sinα\sin{(\pi-\alpha)}=\sin{\alpha}sin(π−α)=sinα
-
cos(π−α)=−cosα\cos{(\pi-\alpha)}=-\cos{\alpha}cos(π−α)=−cosα
-
sin(π+α)=−sinα\sin(\pi+\alpha)=-\sin{\alpha}sin(π+α)=−sinα
-
cos(π+α)=−cosα\cos{(\pi+\alpha)}=-\cos{\alpha}cos(π+α)=−cosα
-
总之,第一象限全是正的,第三象限全是负的
倒数关系
正弦(sine)×余割(co−secant)=1正割(secant)×余弦(co−sine)=1正切(tangent)×余切(co−tangent)=1正弦(sine)\times余割(co-secant)=1 \\正割(secant)\times余弦(co-sine)=1 \\ 正切(tangent)\times余切(co-tangent)=1 正弦(sine)×余割(co−secant)=1正割(secant)×余弦(co−sine)=1正切(tangent)×余切(co−tangent)=1
| tan·gent | co·tan·gent | se·cant | co·se·cant |
|---|---|---|---|
| /ˈtanjənt/ | /kōˈtanjənt/ | /ˈsēˌkant,ˈsēˌkənt/ | /kōˈsēkənt/ |
| 正切 | 余切 | 正割 | 余割 |
六种三角函数间的转换关系
- 正弦余弦&正割余割&正切余切间的转换(π2\frac{\pi}{2}2π)

小结
-
π2−α\frac{\pi}{2}-\alpha2π−α:关于y=xy=xy=x对称
-
关于y=xy=xy=x对称的两点P1=(x1,y1),P2=(x2,y2)P_1=(x_1,y_1),P2=(x_2,y_2)P1=(x1,y1),P2=(x2,y2)坐标关系:
- x1=y2x_1=y_2x1=y2
- x2=y1x_2=y_1x2=y1
Reflections
Shifts and periodicity