餐饮网站开发背景免费网站模板

二分

二分法是我们在高中数学就学习过的一种思想，他也是一种效率较高的查找算法，在编写代码的过程中，初学者很容易就会陷入死循环

二分的基本步骤如下

第一步是需要确定一个区间，使得我们的目标值一定是在区间中出现的

第二步需要确定一个性质，使得这个性质满足两点，第一点是可以根据这个性质把这个区间分为左和右连续的两段，第二点是我们最终的答案一定是二分的某一个分界点（绝大多数）

整数二分是很容易出现死循环的一种情况，因为整数是离散的，因此对应的答案在边界的情况也是两种

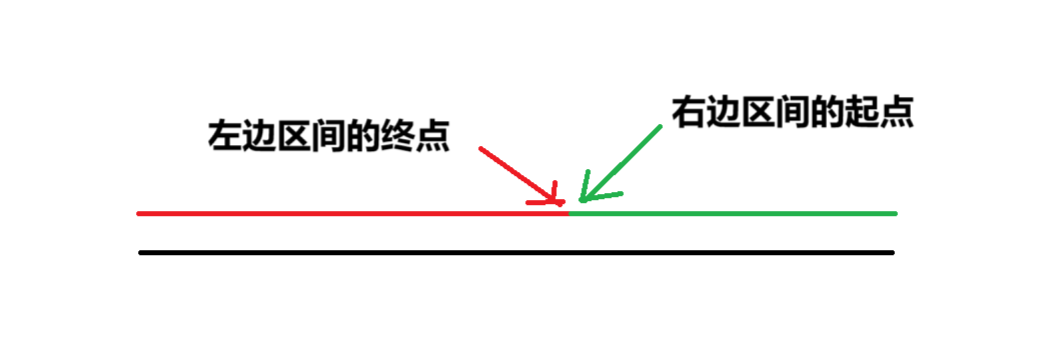
其实相对应的，我们也可以将二分分为两大类，一种是答案在左边的终点，另一种是答案在右边的起点

我们来具体看一下这两种问题是如何二分的

第一类

目标值在红色区间的右端点

我们把区间进行标注，如图

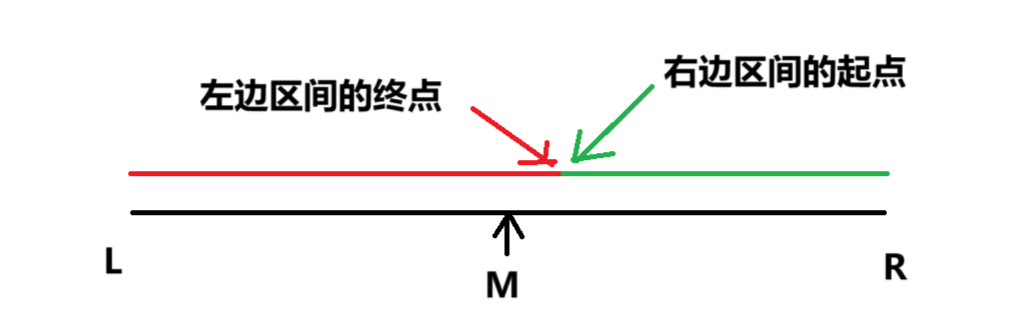
M是L和R的中点，其实就把区间[L,R]分成[L,M-1]和[M,R]

分成两段之后，我们只需要判断M的颜色(性质)，如果是在红色区间，就说明目标值一定在绿色区间[M,R]内，否则说明目标值在红色区间[L,M-1]内

对应到代码上，我们可以这样写

while (L < R)
{M = (L + R + 1) / 2;if (M == '红')L = M;elseR = M - 1;
}

这里需要注意的就是，当答案在左边区间的最后一位时，由于C/C++会自动下取整，这里算中点时就需要补上1，这样就不会漏判（死循环）了，当然这里也可以更改判断条件（例如L<=R），同样也不会出现死循环

这里有个简单的判断是否需要补上1，就是看我们在判断的时候如果写的是L=M，加上1就可以了

第二类

目标值是绿色区间的左端点

将[L,R]分成[L,M]和[M+1,R]，如果M是绿色，说明目标值在红色区间[L,M]，否则就是在绿色区间[M+1,R]

这里我们可以给出相应的代码

while (L < R)
{M = (L + R) / 2;if (M == '绿')R = M;elseL = M + 1;
}

同样的，我们也是只要看判断之后的赋值语句即可，当L = M时，则需要加上1，当R = M时，则不需要加

前缀和

前缀和其实是一种快捷的求和的思想，是用于求一个静态区间的任意位置之间的所有数的和的思想

这里我们直接结合最基础的例题来理解

原题链接

795. 前缀和

题目描述

输入一个长度为 n 的整数序列。

接下来再输入 m 个询问，每个询问输入一对 l,r。

对于每个询问，输出原序列中从第 l 个数到第 r 个数的和。

输入格式

第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数数列。

接下来 m 行，每行包含两个整数 l 和 r，表示一个询问的区间范围。

输出格式

共 m 行，每行输出一个询问的结果。

数据范围

1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000

输入样例：

5 3
2 1 3 6 4
1 2
1 3
2 4 

输出样例：

3
6
10 

题目分析

这里就是给出一个静态序列，有m次询问，每次给一对l和r，需要分别输出从l到r的总和

如果我们暴力做的话，就是每一次都需要从l加到r，并且每一次循环都是O(n)的时间复杂度

一旦当询问次数较大时，时间效率就会非常低

那么这时我们就会需要用到前缀和的思想，他非常的基础和重要，也是笔者最先开始学习的算法之一

我们把之前的那个静态序列标记为$a_i$,表示第i项，然后我们来构建一个新的序列$s_i$，代表他是原序列中前i个数字的和

其中$s_i=a_1+a2+\cdots +a_i$

特殊规定$s_0=0$

这样我们就可以发现一个规律

$s_i=s_{i-1}+a_i$

我们可以根据这个公式递推出s序列中的所有数字

for(int i = 1; i <= n; i++)
{s[i] = s[i-1] + a[i];
}

这一步骤就叫做前缀和，也是我们之后求和的预处理工作

当我们想算从l到r的和时可以这样$a_l+a_{l+1}+a_{l+2}+\cdots +a_r$

$=a_1+a_2+\cdots +a_{l-1}+a_l+a_{l+1}+a_{l+2}+\cdots +a_r-a_1-a_2-\cdots -a_{l-1}$

$=s_r-s_{l-1}$

所以当我们预处理结束之后，我们只需要计算两个数的差即可，这样的时间复杂度就达到了O(1)，是质的飞跃

对于计算区间和还有其他的方法，例如树状数组和线段树，这个我们以后会讲解，而对于前缀和来说，他的局限性就在于序列只能是静态的序列，一旦其中的某个数值被修改，就需要重新计算前缀和，而树状数组和线段树是可以实现边查边算的

示例代码

#include<iostream>
using namespace std;const int N = 1e5+10; // 数据范围
int n,m;
long long arr[N]; // 原数组
long long pre[N]; // 前缀和数组int main()
{cin >> n >> m;for(int i=1;i<=n;i++) // 数据输入{cin>>arr[i];pre[i] = pre[i-1] + arr[i]; // 前缀和初始化}while(m--){int l,r;cin>>l>>r;cout<<pre[r] - pre[l-1]<<'\n';}return 0;
}