优秀电子商务网站正规网站建设服务

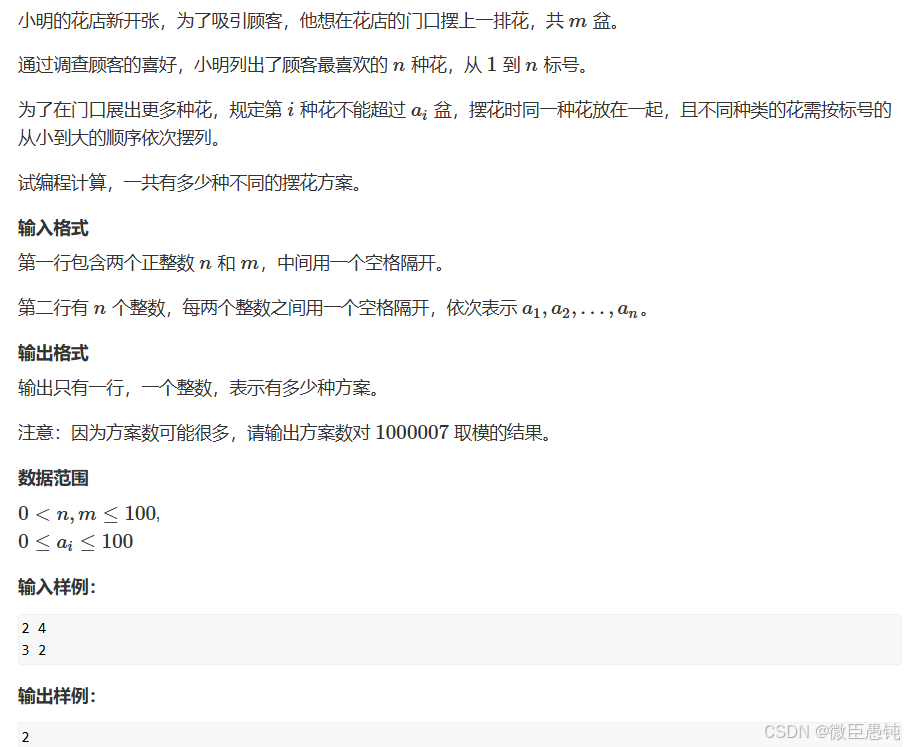
📌题目描述

📌解题思路

📌完整代码

 📌举例

---

📌题目描述

📌解题思路

动态规划（DP） 问题，核心是 “前 i 种物品，每种物品最多可以使用x 次，组成总和 j 的方案数”

 

 

dp[i, j] = dp[i - 1, j] + dp[i - 1, j - 1] + ... + dp[i - 1, j - a[i]]

 

📌完整代码

#include <iostream>using namespace std;const int N = 110, mod = 1000007;int n, m, dp[N][N];int main()
{cin >> n >> m;dp[0][0] = 1; // 初始化，0个物品凑成0的方案数为1for (int i = 1; i <= n; i++){int x;cin >> x;  // 读取物品 i 可用的最大次数for (int j = 0; j <= m; j++){// k 不能超过当前背包容量 j，也不能超过当前物品数量 xfor (int k = 0; k <= j && k <= x; k++){dp[i][j] = (dp[i][j] + dp[i - 1][j - k]) % mod;}}}cout << dp[n][m] << endl; // 输出方案数return 0;
}

• 三重循环：
  • 外层 i（遍历 n 个物品），
  • 中层 j（遍历 0~m 的总和），
  • 内层 k（最多遍历 x 次）。
• 时间复杂度：O(n × m × x)
  • 在 x 取较大值时，可能会 超时。

 📌举例

n = 3（3种花），m = 5（总共需要摆放5朵花），每种花的数量限制如下：

• 第1种花最多可以用3次。
• 第2种花最多可以用2次。
• 第3种花最多可以用1次。

迭代第1种花

dp[1][0] = 1
dp[1][1] = 1
dp[1][2] = 1
dp[1][3] = 1
dp[1][4] = 0
dp[1][5] = 0

 迭代第2种花

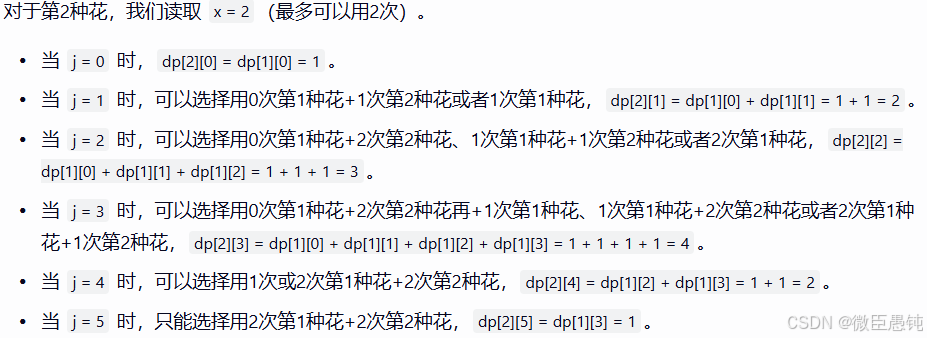
dp[2][0] = 1
dp[2][1] = 2
dp[2][2] = 3
dp[2][3] = 4
dp[2][4] = 2
dp[2][5] = 1

 迭代第3种花

dp[3][0] = 1
dp[3][1] = 3
dp[3][2] = 6
dp[3][3] = 10
dp[3][4] = 11
dp[3][5] = 10

最终，dp[3][5] = 10，表示用3种花摆放5朵花的方案数为10。