北京南昌网站建设优化排名推广教程网站

介绍

  我们已经学习了简单的分类任务和回归任务，也认识了逻辑回归和正则化等技巧，已经可以搭建一个简单的神经网络模型了。
  神经网络模仿人类神经元，进行运算、激活、传递等一系列行为，最终得到结果。这些将在之后详细讲述

模型结构

层（Layer）

  一个完整的神经网络由许多层（layer）组成，除了输入层和输出层，中间的层被统称为隐藏层（Hidden Layers），具体根据功能不同有不同的名字。

神经元

  一个层由许多神经元组成，一层中神经元的数量称为这一层的宽度。
  比如，样本特征有“桌子的长 $a$”和“桌子的宽 $b$”，标签为"桌子的面积 $s$"，则我们可以画出这样的图（举个例子）：

  每一个神经元要做的最基本的事情，就是获取上一个神经元的输入，经过计算，给出一个信号给下一个神经元。

前向传播

  前向传播就是接收输入后，经过一系列神经元的计算，再输出的整个过程。最简单的，我们设每个神经元使用最简单的线性回归模型：

输入向量 $x^{(i)}$
$f_j^{(i)}(x^{(i)})=w_j^{(i)}\cdot x^{(i)}+b_j^{(i)}$
这里$w_j^{(i)}$和$b_j^{(i)}$都是神经元上附带的参数，$i$是层的编号，$j$是神经元的编号

  通常计算出$f$后，得到的结果会再经过一个激活函数$g$，来实现非线性的拟合，我们以$Sigmoid$函数为例：

$g(z)=\frac{1}{1+e^{-z}}$

  回顾一下$Sigmoid$函数的性质：

$g^{\prime }(z)=g(z)\ast [1-g(z)]$

  然后这一层得到的结果作为输入进入下一层：

$x^{(i+1)}=\left[\begin{array}{c}g(f_1^{(i)}(x^{(i)}))\\ g(f_2^{(i)}(x^{(i)}))\\ ...\\ g(f_{k_i}^{(i)}(x^{(i)}))\end{array}\right]$

  除了Sigmoid函数，Relu函数也经常被使用：

$g(z)=\{\begin{array}{l}zifz\ge 0,\\ 0ifz<0\end{array}=max(0,z)$

  由于它的导数非常简单，可以加速收敛；更重要的是它可以避免梯度消失问题，这个之后再讲。

  在最后的输出层时，我们通常使用另一个激活函数$Softmax$

$Softmax:x=[x_1,x_2,...,x_k]\to y=[y_1,y_2,...,y_k]$
      $suchthat{y}_i=\frac{x_i}{{\sum }_{j=1}^k{x}_j}$
即按比例将结果转化为概率的形式，且总和为$1$
因此得到的$y_i$有时也会写为$P(y=i|x)$

反向传播

  在训练模型过程中，我们会将样本集丢进初始化的模型中，得到预测值，通过预测值与标签（真实值）的差异来调整模型；在神经网络中也是如此。我们这里采用梯度下降的方式，且假定损失函数为均方误差，前向传播的过程如下：

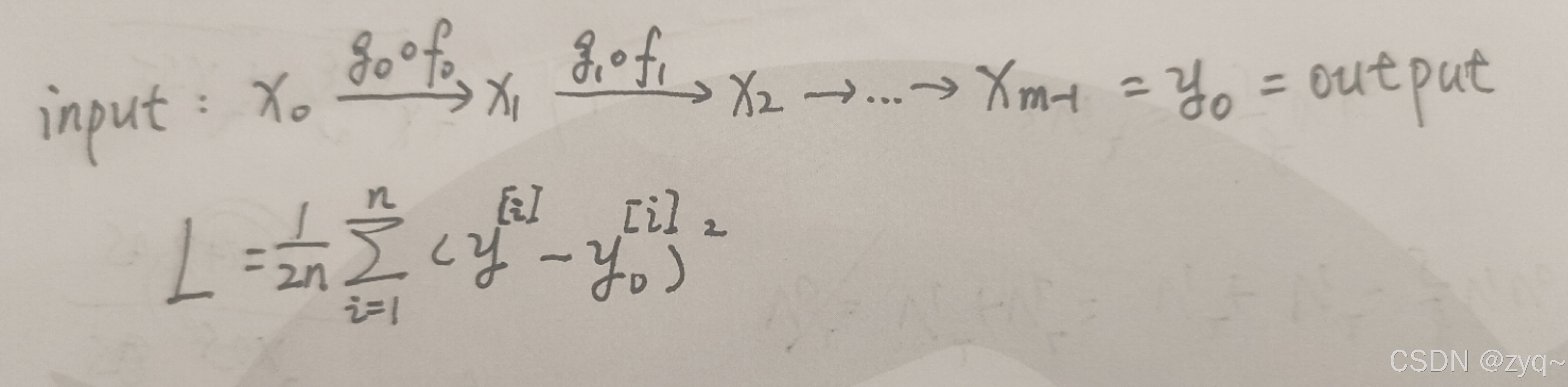
  于是，根据梯度下降，有：

$w_j^{(i)}=w_j^{(i)}-\alpha \frac{\delta L}{\delta w_j^{(i)}}$
$b_j^{(i)}=w_j^{(i)}-\alpha \frac{\delta L}{\delta b_j^{(i)}}$

  其中$\alpha$为学习率，$\delta$是偏导，回顾一下每个神经元的运算：

$z_j^{(i)}=f_j^{(i)}(x^{(i)})=w_j^{(i)}\cdot x^{(i)}+b_j^{(i)}$
$x_j^{(i+1)}=g(z_j^{(i)})$，其中假设每个神经元用的都是g为$sigmoid$函数，不作区分
 
应用链式法则：
$\frac{\delta L}{\delta w_j^{(i)}}=\frac{\delta L}{\delta x_j^{(i+1)}}\ast \frac{\delta x_j^{(i+1)}}{\delta z_j^{(i)}}\ast \frac{\delta z_j^{(i)}}{\delta w_j^{(i)}}$
$=\frac{\delta L}{\delta x_j^{(i+1)}}\ast x_j^{(i+1)}\ast (1-x_j^{(i+1)})\ast x_j^{(i)}$
$\frac{\delta L}{\delta b_j^{(i)}}=\frac{\delta L}{\delta x_j^{(i+1)}}\ast \frac{\delta x_j^{(i+1)}}{\delta z_j^{(i)}}\ast \frac{\delta z_j^{(i)}}{\delta b_j^{(i)}}$
$=\frac{\delta L}{\delta x_j^{(i+1)}}\ast x_j^{(i+1)}\ast (1-x_j^{(i+1)})$
 
计算$\frac{\delta L}{\delta x_j^{(i)}}$:
$\frac{\delta L}{\delta x_j^{(i)}}=\frac{\delta L}{\delta x_j^{(i+1)}}\ast \frac{\delta x_j^{(i+1)}}{\delta x_j^{(i)}}$
$=\frac{\delta L}{\delta x_j^{(i+1)}}\ast x_j^{(i+1)}\ast (1-x_j^{(i+1)})\ast w_j^{(i)}$
最后一层，这里$y$是标签，$y^{{}^{\prime }}$是预测值：
$\frac{\delta L}{\delta x_j^{(m-1)}}=\frac{\delta L}{\delta y_j^{{}^{\prime }}}=\frac{1}{n}\ast (y_j^{{}^{\prime }}-y_j)$
使用归纳（反向递推），即可得到$\frac{\delta L}{\delta x_j^{(i)}}$

Q1: 为什么要用向量

  因为电脑在处理向量或矩阵时能进行批量运算，在计算数量级很大时能显著节约训练时间。

Q2: 不用激活函数会发生什么

  如果不用激活函数，意味着每一个节点都是进行线性变化，而线性变化的复合依然是线性变化，故再多的神经元也无法拟合出更好的结果。