电商网站设计规划书太原seo关键词排名优化

动态规划（Dynamic Programming）：是运筹学的一种最优化方法，只不过在计算机问题上应用比较多

DP常见步骤：

1. 暴力递归/穷举
2. 记忆化搜索（傻缓存 + 递归）,使用备忘录/ DP Table 来优化穷举过程
3. 严格表结构（整理缓存之间的关系，如dp[i] = dp[i - 1]）

例子

509.斐波那契数

1.暴力递归

int fib(int N) {if (N == 1 || N == 2){return 1;}return fib(N - 1) + fib(N - 2);
}

2.记忆化搜索（加缓存）

int fib(int N) {// 备忘录全初始化为 0int[] memo = new int[N + 1];// 进行带备忘录的递归return dp(memo, N);
}// 带着备忘录进行递归
int dp(int[] memo, int n) {// base caseif (n == 0 || n == 1) return n;// 已经计算过，不用再计算了if (memo[n] != 0) return memo[n];memo[n] = dp(memo, n - 1) + dp(memo, n - 2);return memo[n];
}

3.严格表结构（缓存+状态转移方程）

int fib(int N) {if (N == 0) return 0;int[] dp = new int[N + 1];// base casedp[0] = 0; dp[1] = 1;// 状态转移for (int i = 2; i <= N; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[N];
}

4.空间压缩（优化）

由 状态转移方程可知，f(n) 只和 f(n-1) 和 f(n-2) 有关，使用「滚动数组思想」可以把空间复杂度优化成 O(1)

    int fib(int n) {if (n < 2) {return n;}int p = 0, q = 0, r = 1;for (int i = 2; i <= n; ++i) {p = q; q = r; r = p + q;}return r;}

基础类DP

70.爬楼梯

经典动态规划

class Solution {public int climbStairs(int n) {if (n == 1){return 1;}int[] dp = new int[n + 1];dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
}

空间压缩

class Solution {public int climbStairs(int n) {if (n == 1) {return 1;}int prev = 1;int cur = 2;int next = 0;for (int i = 3; i <= n; i++) {next = cur + prev;prev = cur;cur = next;}return cur;}
}

746.使用最小花费爬楼梯

class Solution {public int minCostClimbingStairs(int[] cost) {int[] dp = new int[cost.length + 2];dp[1] = 0;dp[2] = 0;for (int i = 3; i <= cost.length + 1; i++) {dp[i] = Math.min(dp[i - 1] + cost[i - 2], dp[i - 2] + cost[i - 3]);}return dp[cost.length + 1];}
}

空间压缩

class Solution {public int minCostClimbingStairs(int[] cost) {int prev = 0;int cur = 0;int next = 0;for (int i = 2; i <= cost.length; i++) {next = Math.min(prev + cost[i - 2], cur + cost[i - 1]);prev = cur;cur = next;}return cur;}
}

62.不同路径

class Solution {public int uniquePaths(int m, int n) {if (m <= 0 || n <= 0) {return 0;}int[][] dp = new int[m][n];// base casefor (int i = 0; i < m; i++) {dp[i][0] = 1;}for (int i = 0; i < n; i++) {dp[0][i] = 1;}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
}

 路径压缩

class Solution {public int uniquePaths(int m, int n) {if (m <= 0 || n <= 0) {return 0;}int[] dp = new int[n];// base caseArrays.fill(dp, 1);for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[j] += dp[j - 1];}}return dp[n - 1];}
}

63.不同路径 II

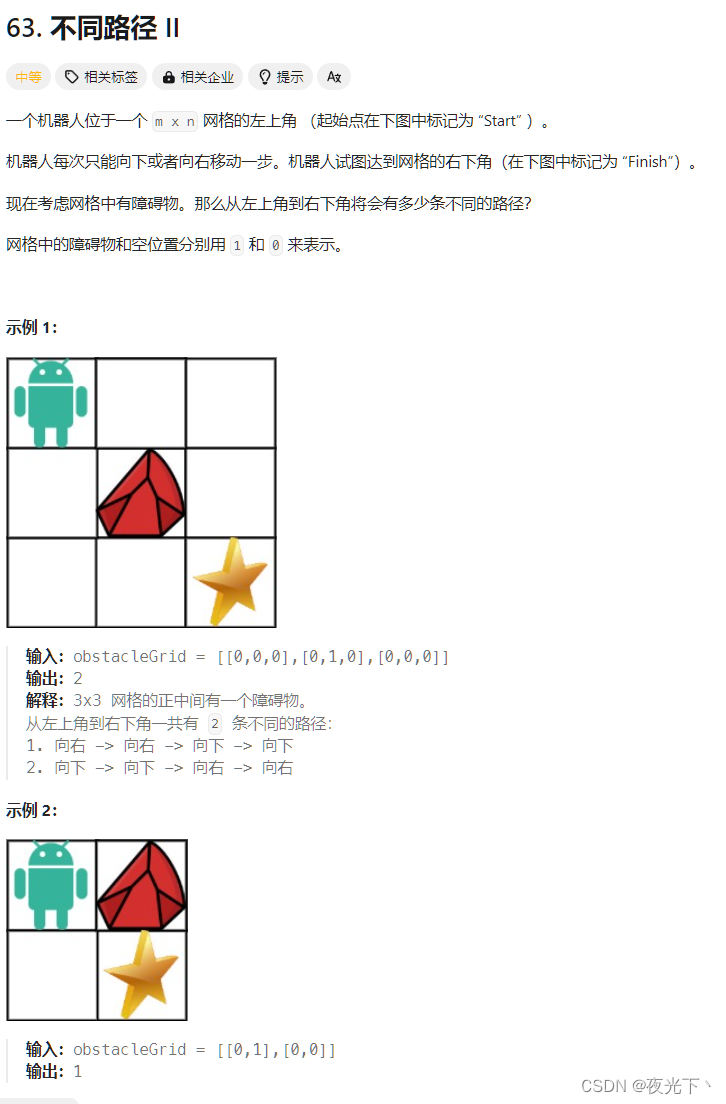
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int row = obstacleGrid.length;int col = obstacleGrid[0].length;int[][] dp = new int[row][col];for (int i = 0; i < row; i++) {if (obstacleGrid[i][0] == 1){break;}dp[i][0] = 1;}for (int i = 0; i < col; i++) {if (obstacleGrid[0][i] == 1){break;}dp[0][i] = 1;}for (int i = 1; i < row; i++) {for (int j = 1; j < col; j++) {dp[i][j] = obstacleGrid[i][j] == 1 ? 0 : dp[i - 1][j] + dp[i][j - 1];}}return dp[row - 1][col - 1];}
}

空间压缩

class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int row = obstacleGrid.length;int col = obstacleGrid[0].length;if (obstacleGrid[0][0] == 1 || obstacleGrid[row - 1][col - 1] == 1) {return 0;}int[] dp = new int[col];dp[0] = 1;for (int j = 1; j < col; j++) {if (obstacleGrid[0][j] == 1) {break;}dp[j] = 1;}for (int i = 1; i < row; i++) {dp[0] = (obstacleGrid[i][0] == 1 || dp[0] == 0) ? 0 : 1;for (int j = 1; j < col; j++) {dp[j] = obstacleGrid[i][j] == 1 ? 0 : dp[j] + dp[j - 1];}}return dp[col - 1];}
}

64.最小路径和

class Solution {public int minPathSum(int[][] grid) {int row = grid.length;int col = grid[0].length;int[][] dp = new int[row][col];dp[0][0] = grid[0][0];for (int i = 1; i < row; i++) {dp[i][0] = grid[i][0] + dp[i - 1][0];}for (int i = 1; i < col; i++) {dp[0][i] = grid[0][i] + dp[0][i - 1];}for (int i = 1; i < row; i++) {for (int j = 1; j < col; j++) {dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];}}return dp[row - 1][col - 1];}
}

空间压缩

class Solution {public int minPathSum(int[][] grid) {int row = grid.length;int col = grid[0].length;int[] dp = new int[col];dp[0] = grid[0][0];for (int i = 1; i < col; i++) {dp[i] = grid[0][i] + dp[i - 1];}for (int i = 1; i < row; i++) {dp[0] = dp[0] + grid[i][0];for (int j = 1; j < col; j++) {dp[j] = Math.min(dp[j], dp[j - 1]) + grid[i][j];}}return dp[col - 1];}
}

class Solution {public boolean canPartition(int[] nums) {int sum = 0;int max = 0;for (int num : nums) {sum += num;max = Math.max(max, num);}int half = sum / 2;if (((sum & 1) == 1) || max > half){return false;}boolean[][] dp = new boolean[nums.length][half + 1];// base casedp[0][0] = true; // 第一个元素不选，容量为0时满足的dp[0][nums[0]] = true; // 选择第一个元素for (int i = 1; i < nums.length; i++) {for (int j = 1; j <= half; j++) {// 不选择 num[i]dp[i][j] = dp[i-1][j];// 保证下标不越界if (j - nums[i] >= 0){// 选择 num[i], 看是否能在 [0, i - 1] 这个子区间内找到一部分元素，使得它们的和为 j - nums[i]dp[i][j] |= dp[i - 1][j - nums[i]];}}// 由于状态转移方程的特殊性，提前结束，可以认为是剪枝操作if (dp[i][half]) {return true;}}return dp[nums.length - 1][half];}
}

class Solution {public boolean canPartition(int[] nums) {int sum = 0;int max = 0;for (int num : nums) {sum += num;max = Math.max(max, num);}int half = sum / 2;if (((sum & 1) == 1) || max > half) {return false;}boolean[] dp = new boolean[half + 1];dp[0] = true;for (int i = 1; i < nums.length; i++) {for (int j = half; j >= nums[i]; j--) {dp[j] |= dp[j - nums[i]];}if (dp[half]) {return true;}}return dp[half];}
}

class Solution {public int findTargetSumWays(int[] nums, int target) {int sum = 0;for (int num : nums) {sum += num;}if (Math.abs(sum) < Math.abs(target)) {return 0;}// 因为包含了负数和 0, range: [-sum, sum]int range = 2 * sum + 1;int[][] dp = new int[nums.length][range];dp[0][sum - nums[0]] += 1;dp[0][sum + nums[0]] += 1;for (int i = 1; i < nums.length; i++) {for (int j = -sum; j <= sum; j++) {if (j + nums[i] > sum) {    // 超过 [-sum, sum] 的范围，只能减dp[i][j + sum] = dp[i - 1][j - nums[i] + sum];} else if (j - nums[i] < -sum) { // 超过 [-sum, sum] 的范围，只能加dp[i][j + sum] = dp[i - 1][j + nums[i] + sum];} else {dp[i][j + sum] = dp[i - 1][j - nums[i] + sum] + dp[i - 1][j + nums[i] + sum];}}}return dp[nums.length - 1][sum + target];}
}

class Solution {public int findMaxForm(String[] strs, int m, int n) {int[][][] dp = new int[strs.length + 1][m + 1][n + 1];for (int i = 1; i <= strs.length; i++) {int zeros = containsZero(strs[i - 1]);int ones = strs[i - 1].length() - zeros;for (int j = 0; j <= m; j++) {for (int k = 0; k <= n; k++) {dp[i][j][k] = dp[i - 1][j][k];if (j >= zeros && k >= ones){dp[i][j][k] = Math.max(dp[i][j][k], dp[i - 1][j - zeros][k - ones] + 1);}}}}return dp[strs.length][m][n];}private int containsZero(String str) {int res = 0;for (char c : str.toCharArray()) {if (c == '0') {res++;}}return res;}
}

class Solution {public int findMaxForm(String[] strs, int m, int n) {int[][] dp = new int[m + 1][n + 1];for (int i = 1; i <= strs.length; i++) {int zeros = containsZero(strs[i - 1]);int ones = strs[i - 1].length() - zeros;for (int j = m; j >= 0; j--) {for (int k = n; k >= 0; k--) {if (j >= zeros && k >= ones){dp[j][k] = Math.max(dp[j][k], dp[j - zeros][k - ones] + 1);}}}}return dp[m][n];}private int containsZero(String str) {int res = 0;for (char c : str.toCharArray()) {if (c == '0') {res++;}}return res;}
}