丹徒网站建设游戏推广赚佣金
文章目录
- Gauss模型
- sympy封装
- 实战
sympy.phisics.optics.gaussopt集成了高斯光学中的常见对象,包括光线和光学元件等,有了这些东西,就可以制作一个光学仿真系统。
Gauss模型
高斯光束的基本模型为
E(r,z)=E0ω0ω(z)exp[−r2ω2(z)]exp[−ikz−ikr22R(z)+iζ(z)]E(r,z)=E_0\frac{\omega_0}{\omega(z)}\exp{[-\frac{r^2}{\omega^2(z)}]}\exp\big[-ikz-ik\frac{r^2}{2R(z)}+i\zeta(z)\big] E(r,z)=E0ω(z)ω0exp[−ω2(z)r2]exp[−ikz−ik2R(z)r2+iζ(z)]
其中部分物理量如下,其余物理量在后面列表中列出
- rrr 为径向坐标,以光轴中心为原点
- zzz 为横向坐标,以束腰位置为参考点
- k=2πλk=\frac{2\pi}{\lambda}k=λ2π 为波数
- ω\omegaω 为zzz处光斑半径,此半径以强度降低到轴向1e2\frac{1}{e^2}e21时的半径
sympy封装
sympy中按照高斯光束模型,实现了光束参数类,其构造函数如下
BeamParameter(wavelen, z, z_r=None, w=None, n=1)
wavelen波长z距离束腰的距离w束腰半径z_r瑞利距离n介质折射率
其属性列表如下
| 成员 | 物理意义 | 说明 |
|---|---|---|
w_0 | ω0\omega_0ω0 | 束腰半径,构造函数中的w |
z_r | zr=πω02λz_r=\frac{\pi\omega_0^2}{\lambda}zr=λπω02 | 瑞利距离 |
gouy | ζ(z)=arctanzzr\zeta(z)=\arctan\frac{z}{z_r}ζ(z)=arctanzrz | Gouy 相移 |
w | ω(z)=ω01+(zzr)2\omega(z)=\omega_0\sqrt{1+(\frac{z}{z_r})^2}ω(z)=ω01+(zrz)2 | z处的光斑半径 |
radius | R(z)=z[1+(zrz)2]R(z)=z\big[1+(\frac{z_r}{z})^2\big]R(z)=z[1+(zzr)2] | 波前曲率半径 |
q | q=z+ifq=z+ifq=z+if | 光的复参数 |
divergence | λπω0\frac{\lambda}{\pi\omega_0}πω0λ | 半角扩散 |
此外,waist_approximation_limit为衍射极限,一般为2λπ\frac{2\lambda}{\pi}π2λ。
实战
from sympy.physics.optics import BeamParameter
p = BeamParameter(532e-9, 1, w=1e-3)
print(p.q) # 1 + 1.8796992481203*I*pi
print(p.divergence) # 0.000532/pi
print(p.gouy) # atan(0.532/pi)
print(p.radius) # 1 + 3.53326926338402*pi**2
print(p.w) # 0.001*sqrt(0.283024/pi**2 + 1)
print(p.w_0) # 0.00100000000000000
print(p.waist_approximation_limit) # 1.064e-6/pi
如果让参数z是一个符号,那么其成员变量的表达式也会产生自变量
import sympy
from sympy.abc import x,y,z
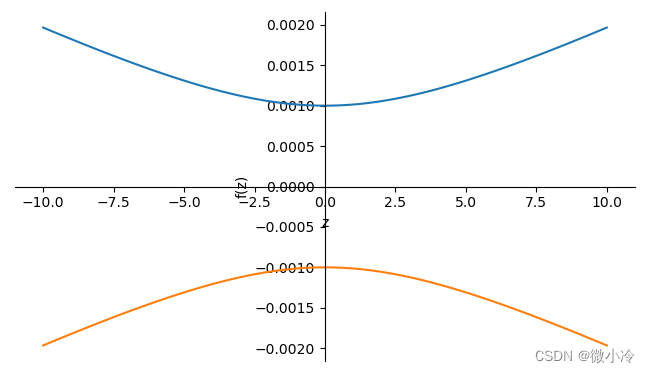
p = BeamParameter(532e-9, z, w=1e-3)
sympy.plot(p.w, -p.w)
得到经典的Gauss光束传播双曲线