外贸营销网站建设方案nba常规赛
AVL 树的概念
也许因为插入的值不够随机,也许因为经过某些插入或删除操作,二叉搜索树可能会失去平衡,甚至可能退化为单链表,造成搜索效率低。

AVL Tree 是一个「加上了额外平衡条件」的二叉搜索树,其平衡条件的建立是为了确保整棵树的深度为 O(log2N)O(log_2N)O(log2N)。
AVL Tree 要求任何节点的左右子树高度相差最多为 1。当违反该规定时,就需要进行旋转来保证该规定。
AVL 树的实现
节点的定义
AVL 树节点的定义比一般的二叉搜索树复杂,它需要额外一个 parent 指针,方便后续旋转。并在每个节点中引入平衡因子,便于判断是否需要旋转。
/// @brief AVL 树节点结构
/// @tparam K 节点的 key 值
/// @tparam V 节点的 value 值
template <class K, class V>
struct AVLTreeNode {AVLTreeNode(const pair<K, V>& kv) : _kv(kv), _parent(nullptr), _left(nullptr), _right(nullptr), _bf(0){}pair<K, V> _kv;AVLTreeNode<K, V>* _parent;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;// 左右子树高度相同平衡因子为:0// 左子树高平衡因子为负// 右子树高平衡因子为正int _bf;
};
接口总览
template<class K, class V>
class AVLTree {typedef AVLTreeNode<K, V> Node;
public:Node* Find(const K& key);bool Insert(const pair<K, V>& kv);private:void RotateR(Node* parent);void RotateL(Node* parent);void RotateLR(Node* parent);void RotateRL(Node* parent);
private:Node* _root = nullptr;
};
查找
AVL 树的查找和普通的搜索二叉树一样:
- 若 key 值大于当前节点的值,在当前节点的右子树中查找
- 若 key 值小于当前节点的值,在当前节点的左子树中查找
- 若 key 值等于当前节点的值,返回当前节点的地址
- 若找到空,查找失败,返回空指针
/// @brief 查找指定 key 值
/// @param key 要查找的 key
/// @return 找到返回节点的指针,没找到返回空指针
Node* Find(const K& key) {Node* cur = _root;while (cur != nullptr) {// key 值与当前节点值比较if (key > cur->_kv.first) {cur = cur->_right;} else if (key < cur->_kv.first) {cur = cur->_left;} else {return cur;}}return nullptr;
}
插入
AVL 的插入整体分为两步:
- 按照二叉搜索树的方式将节点插入
- 调整节点的平衡因子
平衡因子是怎么调整的?
设新插入的节点为 pCur,新插入节点的父节点为 pParent。在插入之前,pParent 的平衡因子有三种可能:0、-1、1。
插入分为两种:
- pCur 插入到 pParent 的左侧,将 pParent 的平衡因子减 1
- pCur 插入到 pParent 的右侧,将 pParent 的平衡因子加 1
此时,pParent 的平衡因子可能有三种情况:0、正负 1、正负 2。
- 0:说明插入之前是正负 1,插入后被调整为 0,满足 AVL 性质插入成功
- 正负 1:说明插入之前是 0,插入后被调整为正负 1,此时 pParent 变高,需要继续向上更新
- 正负 2:说明插入之前是正负 1,插入后被调整为正负 2,此时破坏了规定,需要旋转处理
/// @brief 插入指定节点
/// @param kv 待插入的节点
/// @return 插入成功返回 true,失败返回 false
bool Insert(const pair<K, V>& kv) {if (_root == nullptr) {_root = new Node(kv);return true;}// 先找到要插入的位置Node* parent = nullptr;Node* cur = _root;while (cur != nullptr) {if (kv.first > cur->_kv.first) {parent = cur;cur = cur->_right;} else if (kv.first < cur->_kv.first) {parent = cur;cur = cur->_left;} else {// 已经存在,插入失败return false;}}// 将节点插入cur = new Node(kv);if (kv.first > parent->_kv.first) {parent->_right = cur;cur->_parent = parent;} else {parent->_left = cur;cur->_parent = parent;}// 更新平衡因子,直到正常while (parent != nullptr) {// 调整父亲的平衡因子if (parent->_left == cur) {--parent->_bf;} else {++parent->_bf;}if (parent->_bf == 0) {// 此时不需要再继续调整了,直接退出break;} else if (parent->_bf == 1 || parent->_bf == -1) {// 此时需要继续向上调整cur = parent;parent = parent->_parent;} else if (parent->_bf == 2 || parent->_bf == -2) {// 此时需要旋转处理if (parent->_bf == -2 && cur->_bf == -1) {RotateR(parent);} else if (parent->_bf == 2 && cur->_bf == 1) {RotateL(parent);} else if (parent->_bf == -2 && cur->_bf == 1) {RotateLR(parent);} else if (parent->_bf == 2 && cur->_bf == -1) {RotateRL(parent);} else {assert(false);}// 旋转完了就平衡了,直接退出break;} else {// 此时说明之前就处理错了assert(false);} // end of if (parent->_bf == 0)} // end of while (parent != nullptr)return true;
}
旋转
假设平衡因子为正负 2 的节点为 X,由于节点最多拥有两个子节点,因此可以分为四种情况:
- 插入点位于 X 的左子节点的左子树——左左:右单旋
- 插入点位于 X 的左子节点的右子树——左右:左右双旋
- 插入点位于 X 的右子节点的右子树——右右:左单旋
- 插入点位于 X 的右子节点的左子树——右左:右左双旋

右单旋

假设平衡因子为正负 2 的节点为 parent,parent 的父节点为 pParent,parent 的左子树为 subL,subL 的右子树为 subLR。
右单旋的操作流程:
- 让 subLR 作为 parent 的左子树
- 让 parent 作为 subL 的右子树
- 让 subL 作为整个子树的新根
- 更新平衡因子
/// @brief 进行右单旋
/// @param parent 平衡因子为正负 2 的节点
void RotateR(Node* parent) {Node* pParent = parent->_parent;Node* subL = parent->_left;Node* subLR = parent->_left->_right;// 更改链接关系// 1. subLR 作为 parent 的左子树parent->_left = subLR;if (subLR != nullptr) {subLR->_parent = parent;}// 2. parent 作为 subL 的右子树subL->_right = parent;parent->_parent = subL;// 3. subL 作为整个子树的新根if (parent == _root) {// parent 为 _root,此时令 subL 为 _root_root = subL;subL->_parent = nullptr;} else {// parent 不为 _root,pParent 也就不为空if (parent == pParent->_left) {pParent->_left = subL;} else {pParent->_right = subL;}subL->_parent = pParent;}// 4. 更新平衡因子// 观察上图明显可知subL->_bf = 0;parent->_bf = 0;
}
左单旋
左单旋与右单旋类似,只是方向不同。
假设平衡因子为正负 2 的节点为 parent,parent 的父节点为 pParent,parent 的右子树为 subR,subR 的左子树为 subRL。
左单旋的操作流程:
- 让 subRL 作为 parent 的右子树
- 让 parent 作为 subR 的左子树
- 让 subR 作为整个子树的新根
- 更新平衡因子
/// @brief 进行左单旋
/// @param parent 平衡因子为正负 2 的节点
void RotateL(Node* parent) {Node* pParetn = parent->_parent;Node* subR = parent->_right;Node* subRL = parent->_right->_left;// 更改链接关系// 1. subRL 作为 parent 的右子树parent->_right = subRL;if (subRL != nullptr) {subRL->_parent = parent;}// 2. parent 作为 subR 的左子树subR->_left = parent;parent->_parent = subR;// 3. subR 作为整个子树的新根if (parent == _root) {_root = subR;subR->_parent = nullptr;} else {if (parent == pParetn->_left) {pParetn->_left = subR;} else {pParetn->_right = subR;}subR->_parent = pParetn;}// 4. 更新平衡因子subR->_bf = 0;parent->_bf = 0;
}
左右双旋

假设平衡因子为正负 2 的节点为 parent,parent 的左子树为 subL,subL 的右子树为 subLR。
左右双旋就是对 subL 进行一次左单旋,对 parent 进行一次右单旋。双旋也就完成了,要注意的是双旋后平衡因子的更新。
此时分三种情况:
- 新插入的节点是 subLR 的右子树

- 新插入的节点是 subLR 的左子树
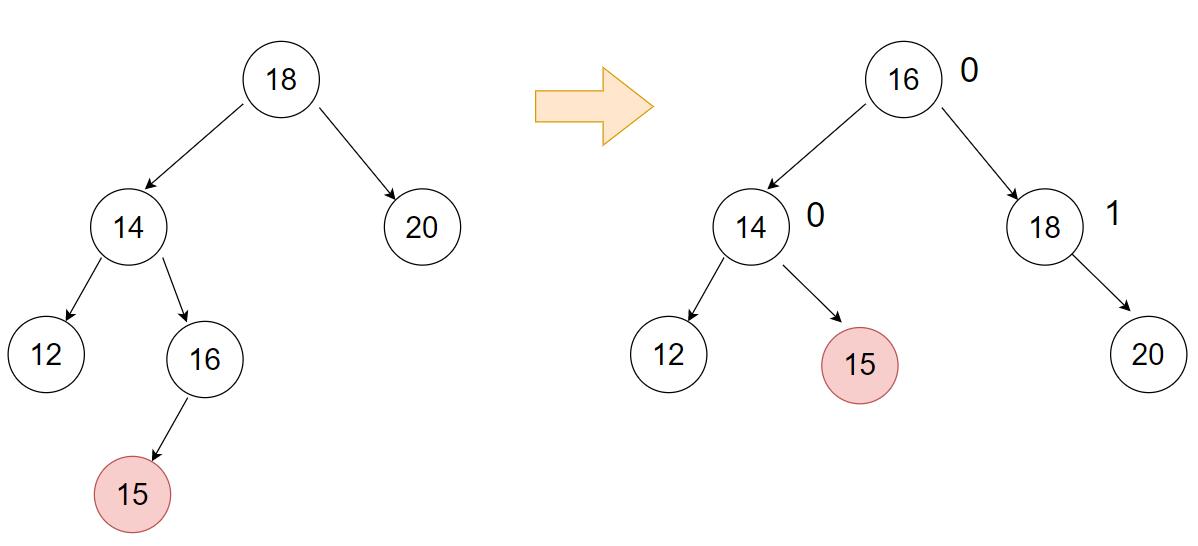
- 新插入的是 subLR
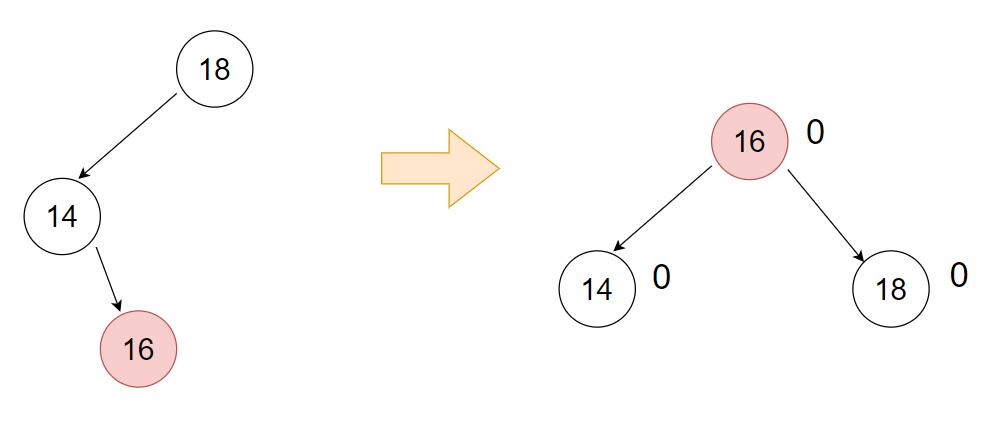
结合上述情况,写出如下代码:
/// @brief 进行左右双旋
/// @param parent 平衡因子为正负 2 的节点
void RotateLR(Node* parent) {Node* subL = parent->_left;Node* subLR = parent->_left->_right;int bf = subLR->_bf;RotateL(subL);RotateR(parent);if (bf == 1) {// 新插入节点是 subLR 的右子树parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;} else if (bf == -1) {// 新插入的节点是 subLR 的左子树parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;} else if (bf == 0) {// 新插入的节点是 subLRparent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;} else {assert(false);}
}
右左双旋
假设平衡因子为正负 2 的节点为 parent,parent 的右子树为 subR,subR 的左子树为 subRL。
右左双旋就是对 subR 进行一次右单旋,对 parent 进行一次左单旋。流程和左右双旋一样,这里就不过多介绍了。
void RotateRL(Node* parent) {Node* subR = parent->_right;Node* subRL = parent->_right->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == 1) {// 新插入节点是 subRL 的右子树parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;} else if (bf == -1) {// 新插入的节点是 subRL 的左子树parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;} else if (bf == 0) {// 新插入的节点是 subRLparent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;} else {assert(false);}
}
