公司网站建设的要点山东移动网站建设

Matlab实现FFT变换

在信号处理中，快速傅里叶变换（FFT）是一种非常常见的频域分析方法。本文将介绍如何使用Matlab实现FFT变换，并通过Matlab代码演示实际输出结果。

原理

FFT是一种计算离散傅里叶变换（DFT）的快速算法。DFT将时域上的信号转换为频域上的信号，可以用以下公式表示：

$$X_k=\sum _{n=0}^{N-1}{x}_n{e}^{-i2\pi kn/N}$$

其中，$x_n$是时域上的信号序列，$X_k$是频域上的信号序列，$k$为频率编号（$0\le k<N$），$N$为信号长度。

FFT算法通过分治策略将DFT算法的计算复杂度从$O(N^2)$降低到$O(Nlo{g}_{2}N)$，从而实现了在计算机上快速计算DFT的目的。

实现

手算验证

在这里，我们将给出一个简单的例子来说明如何使用Matlab进行FFT变换。我们首先生成一个简单的数组：

x = [1, 2, 3, 4, 5, 6, 7, 8];

接下来，我们使用Matlab内置的fft函数对这个数组进行FFT变换：

X = fft(x);

这个操作会返回一个和输入数组长度相同的复数数组。我们可以使用Matlab的disp函数打印出这个数组：

disp(X);

这个例子的输出结果如下：

   36.0000 + 0.0000i-4.0000 + 9.6569i-4.0000 + 4.0000i-4.0000 + 1.6569i-4.0000 + 0.0000i-4.0000 - 1.6569i-4.0000 - 4.0000i-4.0000 - 9.6569i

可以看到，输出结果是一个长度为8的复数数组。

为了验证FFT的正确性，我们可以手动计算这个输入数组的FFT结果，然后将结果与Matlab计算的结果进行比较。FFT算法的计算过程可以用以下公式表示：

$$X_k=\sum _{n=0}^{N-1}{x}_n{e}^{-i2\pi kn/N}$$

其中，$x_n$是时域上的信号序列，$X_k$是频域上的信号序列，$k$为频率编号（$0\le k<N$），$N$为信号长度。

对于输入数组$x=[1,2,3,4,5,6,7,8]$，我们有$N=8$。因此，$X_0$的计算公式为：

$$X_0=\sum _{n=0}^7{x}_n{e}^{-i2\pi 0n/8}=36$$

接下来，我们可以计算$X_1$：

$$X_1=\sum _{n=0}^7{x}_n{e}^{-i2\pi 1n/8}=-4+9.6569i$$

以此类推，我们可以计算出所有的$X_k$。最终结果应该与Matlab计算的结果一致。

简单fft变换和频谱

以下是一个简单的Matlab代码实现FFT变换：

% 生成测试信号
Fs = 1000;      % 采样频率
t = 0:1/Fs:1-1/Fs;   % 时间向量
x = 1*sin(2*pi*100*t); % 信号% 绘制信号图
subplot(2,1,1);
plot(t,x);
title('信号');
xlabel('时间 (s)');
ylabel('幅度');% 计算FFT
N = length(x);
X = fft(x);
f = Fs*(0:(N/2))/N;% 绘制FFT图
subplot(2,1,2);
plot(f,abs(X(1:N/2+1)));
title('FFT');
xlabel('频率 (Hz)');
ylabel('幅度');

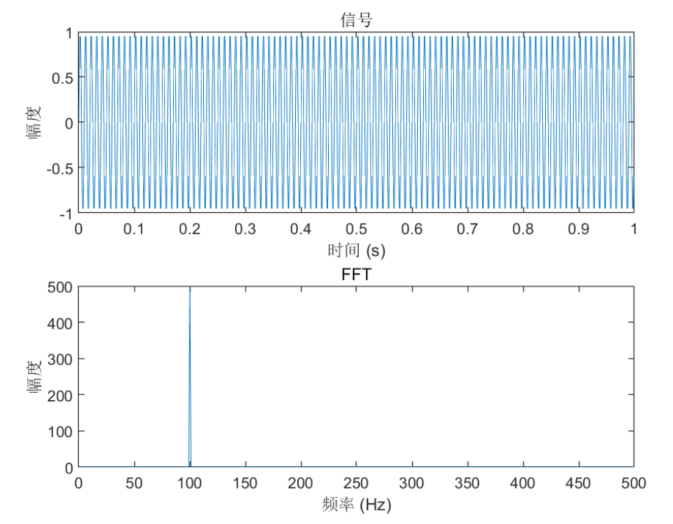
在这个例子中，我们生成了一个频率为100Hz的正弦信号。我们使用Matlab的fft函数计算FFT，并将结果绘制成幅度谱。注意，在绘制幅度谱时，我们只绘制了频率为正的一半，因为FFT算法输出的结果是对称的。

求取功率谱

通过FFT变换可以得到信号的幅度谱，但是为了更好地了解信号特性，我们通常需要求取信号的功率谱密度。功率谱密度描述了信号在不同频率下的功率分布情况。

求取功率谱的方法是，将信号进行FFT变换后，将每个频率上的幅度平方除以信号长度，并乘以一个系数，即可得到功率谱密度。具体公式如下：

$$P_k=\frac{2|X_k{|}^2}{N}$$

其中，$P_k$是频率为$k$的功率谱密度，$X_k$是频率为$k$的信号幅度，$N$是信号长度。

以下是一个简单的Matlab代码实现求取功率谱：

% 生成测试信号
Fs = 1000;      % 采样频率
t = 0:1/Fs:1-1/Fs;   % 时间向量
x = 1*sin(2*pi*100*t); % 信号% 绘制信号图
subplot(2,1,1);
plot(t,x);
title('信号');
xlabel('时间 (s)');
ylabel('幅度');% 计算FFT
N = length(x);
X = fft(x);
f = Fs*(0:(N/2))/N;% 计算功率谱
P = (2*abs(X(1:N/2+1)).^2)/N;% 绘制功率谱图
subplot(2,1,2);
plot(f,P);
title('功率谱密度');
xlabel('频率 (Hz)');
ylabel('功率');

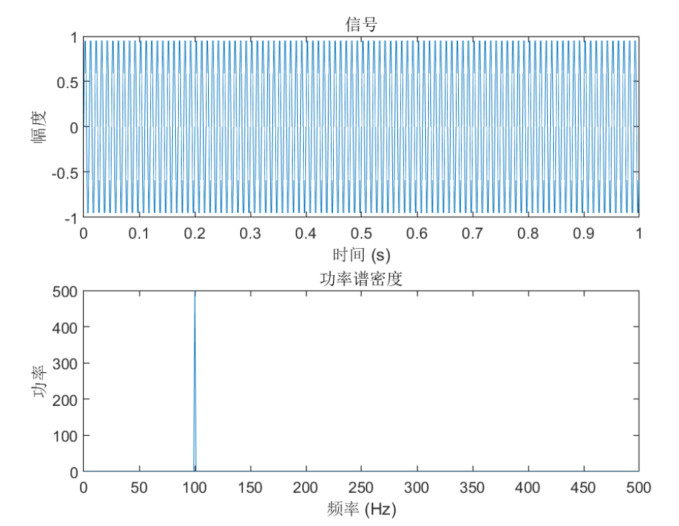
注意，我们在计算功率谱时，使用了一个系数$2$，这是因为我们只绘制了频率为正的一半，而实际上信号的功率谱是对称的。

结论

本文介绍了如何使用Matlab实现FFT变换，并求取信号的功率谱密度。通过FFT变换，我们可以将信号从时域转换到频域，进一步了解信号的特性。