做旅游网站需要注意什么页优化软件
个人主页:点我进入主页
专栏分类:C语言初阶 C语言进阶 数据结构初阶 Linux C++初阶 C++进阶 算法
欢迎大家点赞,评论,收藏。
一起努力,一起奔赴大厂
目录
一.前言
二.插入
三.旋转
3.1右旋
3.2左旋
3.3左右双旋
3.4右左双旋
四.测试
一.前言
在看这篇博客之前需要了解二叉搜索树的相关内容,可以看这篇博客二叉搜索树,AVL树可以看成为了解决二叉搜索树的问题,它保证了左右子树高度差不超过1。本次的内容的重点就是对AVL树的旋转。
二.插入
AVL树的插入规则和二叉搜索树的插入规则类似,左子树都小于父节点,右子树都大于父节点,在这里我们引入了一个平衡因子,我们先插入后然后进行调节平衡因子,平衡因子的计算=右子树的高度-左子树的高度,插入的新节点的平衡因子为0,当插入的节点在父节点的右边,父节点的平衡因子+1,当插入的节点在父节点的左边,父节点的平衡因子-1,当整后父节点的平衡因子为0时直接结束,不需要继续调整,当调整后父节点的平衡因子为+1或者-1时需要继续向上进行调整,当调整后父节点的平衡因子为+2或-2时需要进行旋转。我们看下面的代码实现:
bool insert(const pair<K, V>& kv)
{Node* newnode = new Node(kv);if (_root == nullptr) _root = newnode;else{Node* cur = _root, * parent = nullptr;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first) {parent = cur;cur = cur->_right;}else return false;}if (kv.first < parent->_kv.first) parent->_left = newnode;else parent->_right = newnode;newnode->_parent = parent;//调整平衡因子while (parent){if (newnode == parent->_left) parent->_bf--;else parent->_bf++;if (parent->_bf == 0) break;else if (parent->_bf == 1 || parent->_bf == -1){newnode = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == 2 && newnode->_bf == 1){RatoteL(parent);}else if (parent->_bf == -2 && newnode->_bf == -1){RatoteR(parent);}else if (parent->_bf == 2 && newnode->_bf == -1){RatoteRL(parent);}else if (parent->_bf == -2 && newnode->_bf == 1){RatoteLR(parent);}else{assert(false);}break;}else{assert(false);}}}return true;
}三.旋转
旋转有4种方式:向右旋转,向左旋转,左右双旋,右左双旋这四种
3.1右旋
看下面的抽象图

当n=0时全图为
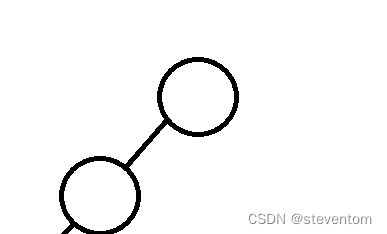
当n=1时全图为

当n=2时我们有3种,但是在a的位置能放第3种,因为别的会自动进行旋转,b和c这三种都可以
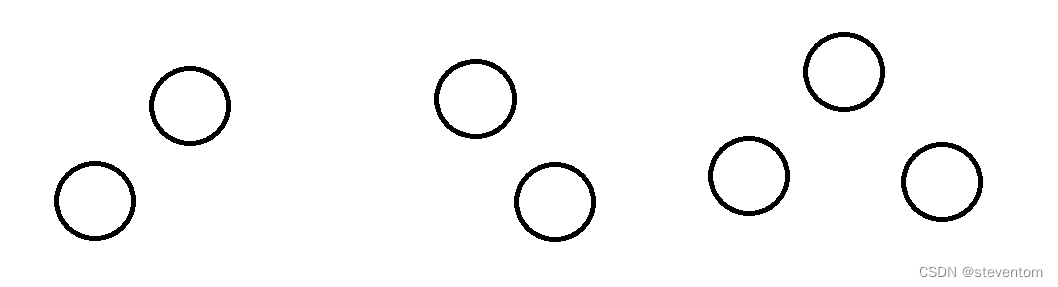
当n=3时就会更多,所以这是列举不完的,针对右旋我们以下面这张图为例:

我们经过右旋后转化成下面的样子,针对的主要就是这几个节点
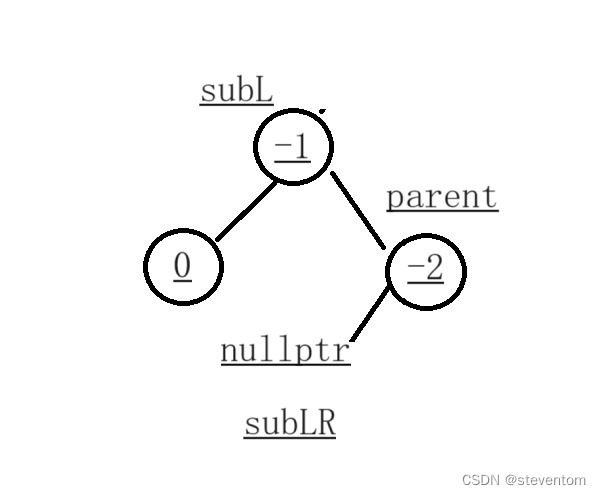
在旋转的过程中需要注意的是,parent节点是不是根节点,注意调整后subL节点的的父节点的调整,还有一点就是subLR是否为空节点,调整后需要将subL节点和parent节点的bf值改为0,我们看下面的代码:
void RatoteR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;subL->_right = parent;parent->_left = subLR;Node* ppNode = parent->_parent;subL->_parent = parent->_parent;parent->_parent = subL;if (subLR)subLR->_parent = parent;if (parent == _root){_root = subL;}else{if (ppNode->_left == parent)ppNode->_left = subL;elseppNode->_right = subL;}subL->_bf = parent->_bf = 0;}3.2左旋
左旋的代码和右旋的类似,不过需要调节的平衡因子为2和1,我们看下面的图片
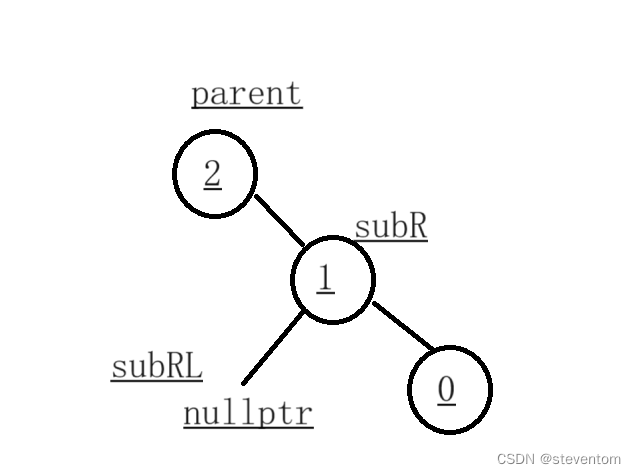
我们直接上代码:
void RatoteL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;parent->_parent = subR;subR->_left = parent;subR->_parent = ppNode;if (parent == _root){_root = subR;}else{if (ppNode->_left == parent)ppNode->_left = subR;elseppNode->_right = subR;}subR->_bf = parent->_bf = 0;
}
void RatoteRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RatoteR(subR);RatoteL(parent);if (bf == 1){parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;}}3.3左右双旋
左右双旋的图片可以看为下面的抽象图:

当我们在b位置插入后再旋转,可以得到:

当我们插入到c位置后再经过旋转,可以得到:
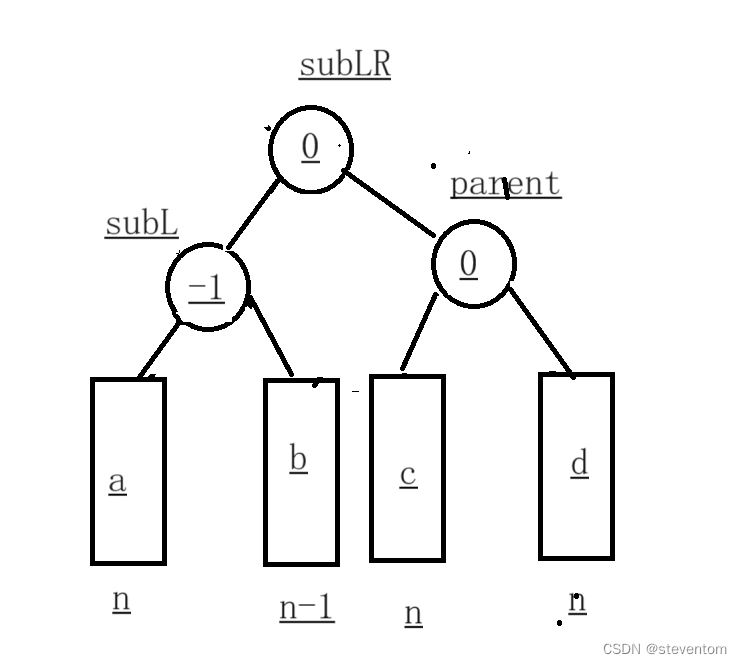
当只旋转一次就会做一次镜像旋转,我们先让subL节点左旋,然后让parent右旋,然后进行调节平衡因子,我们看代码:
void RatoteLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RatoteL(subL);RatoteR(parent);if (bf == 1){subL->_bf = -1;}else if (bf == -1){parent->_bf = 1;}
}3.4右左双旋
这个和左右双旋类似,我们直接看代码:
void RatoteRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RatoteR(subR);RatoteL(parent);if (bf == 1){parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;}}四.测试
我们直接上代码:
public: void InOrder(){_InOrder(_root);}bool IsBalance(){return _IsBalance(_root);}
private:void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << "->" << root->_kv.second << endl;int left = _height(root->_left);int right = _height(root->_right);int sub = abs(left - right);cout << "bf-> " << sub<<endl;if (sub >= 2) cout<<"key-> "<< root->_kv.first << endl;_InOrder(root->_right);}int _height(Node* root){if (root == nullptr)return 0;int x = 1 + _height(root->_left);int y = 1 + _height(root->_right);return max(x , y);}bool _IsBalance(Node* root){ if (root == nullptr) return true;int left = _height(root->_left);int right = _height(root->_right);if (abs(right - left) >= 2){return false;}return _IsBalance(root->_left) && _IsBalance(root->_right);}测试代码:
int main()
{srand(0);AVLTree<int, int> a;vector<int> v;for (int i = 0; i < 1000000; i++){int num = rand() + i;v.push_back(num);}cout << a.IsBalance() << endl;return 0;
}运行可以看到:

