免费不需要vip的追剧软件西安seo经理

算法思想

粒子群算法（Particle Swarm Optimization）

优点:
1）原理比较简单，实现容易，参数少。
缺点:
1）易早熟收敛至局部最优、迭代后期收敛速度慢的。

算法拓展

针对标准PSO的缺点，通常有如下的改进：

1. 实现参数的自适应变化。
2. 引入一些其他机制。比如随机的因素,速度、位置的边界变化-后期压缩最大速度等。
3. 结合其他智能优化算法:遗传算法、免疫算法、模拟退火算法等等，帮助粒子跳出局部最优，改善收敛速度。

matlab代码

二维下

%% 初始化种群  
clear
%% Sphere
clear
f= @(x) x .* sin(x) .* cos(2 * x) - 2 * x .* sin(3 * x) +3 * x .* sin(4 * x); % 函数表达式    % 求这个函数的最大值  N = 20;                         % 初始种群个数  
d = 1;                          % 可行解维数  
ger = 100;                      % 最大迭代次数       
limit = [0, 50];               % 设置位置参数限制  
vlimit = [-10, 10];               % 设置速度限制  
w = 0.8;                        % 惯性权重  
c1 = 0.5;                       % 自我学习因子  
c2 = 0.5;                       % 群体学习因子   
figure(1);ezplot(f,[0,0.01,limit(2)]);   %曲线x = limit(1) + (  limit( 2 ) -  limit( 1)  ) .* rand(N, d);%初始种群的位置v = rand(N, d);                  % 初始种群的速度  
xm = x;                          % 每个个体的历史最佳位置  
ym = zeros(1, d);                % 种群的历史最佳位置  
fxm = ones(N, 1)*inf;               % 每个个体的历史最佳适应度  
fym = inf;                       % 种群历史最佳适应度  
hold on  
plot(xm, f(xm), 'ro');title('初始状态图');  
figure(2)  
%% 群体更新  
iter = 1;  
% record = zeros(ger, 1);          % 记录器  
while iter <= ger  fx = f(x) ; % 个体当前适应度     for i = 1:N        if fx(i)  <fxm(i) fxm(i) = fx(i);     % 更新个体历史最佳适应度  xm(i,:) = x(i,:);   % 更新个体历史最佳位置(取值第i行的所有列)  end   end  if  min(fxm)  < fym [fym, nmin] = min(fxm);   % 更新群体历史最佳适应度  ym = xm(nmin, :);      % 更新群体历史最佳位置  end  v = v * w + c1 * rand * (xm - x) + c2 * rand * (repmat(ym, N, 1) - x);% 速度更新  % 边界速度处理  v(v > vlimit(2)) = vlimit(2);  %可以根据括号中的条件决定是否赋值v(v < vlimit(1)) = vlimit(1);  x = x + v;% 位置更新  % 边界位置处理  x(x > limit(2)) = limit(2);  x(x < limit(1)) = limit(1);  record(iter) = fym;%最大值记录  x0 = 0 : 0.01 : limit(2);  %1行3列的数组subplot(1,2,1)plot(x0, f(x0), 'b-', x, f(x), 'ro');title('状态位置变化')subplot(1,2,2);plot(record);title('最优适应度进化过程')  pause(0.01)  iter = iter+1;  end  x0 = 0 : 0.01 : limit(2);  
figure(4);plot(x0, f(x0), 'b-', x, f(x), 'ro');title('最终状态位置')  
disp(['最大值：',num2str(fym)]);  
disp(['变量取值：',num2str(ym)]);  

三维下

%% 初始化种群  
clear
clc
f = @(x,y)   20 +  x.^2 + y.^2 - 10*cos(2*pi.*x)  - 10*cos(2*pi.*y) ;%[-5.12 ,5.12 ]x0 = [-5.12:0.05:5.12];
y0 = x0 ;
[X,Y] = meshgrid(x0,y0);
Z =f(X,Y)  ;
figure(1); mesh(X,Y,Z);  
colormap(parula(5));N = 50;                         % 初始种群个数  
d = 2;                          % 可行解维数  
ger = 100;                      % 最大迭代次数       
limit = [-5.12,5.12];               % 设置位置参数限制  
vlimit = [-.5, .5];               % 设置速度限制  
w = 0.8;                        % 惯性权重  
c1 = 0.5;                       % 自我学习因子  
c2 = 0.5;                       % 群体学习因子   x = limit(1) + (  limit( 2 ) -  limit( 1)  ) .* rand(N, d);%初始种群的位置  v = rand(N, d);                  % 初始种群的速度  
xm = x;                          % 每个个体的历史最佳位置  
ym = zeros(1, d);                % 种群的历史最佳位置  
fxm = ones(N, 1)*inf;               % 每个个体的历史最佳适应度   
fym = inf;                       % 种群历史最佳适应度  
% record = zeros(ger,1);
hold on 
% [X,Y] = meshgrid(x(:,1),x(:,2));
% Z = f( X,Y ) ;
scatter3( x(:,1),x(:,2) ,f( x(:,1),x(:,2) ),'r*' );
figure(2)  
record=[];%% 群体更新  
iter = 1;  
% record = zeros(ger, 1);          % 记录器  
while iter <= ger  fx = f( x(:,1),x(:,2) ) ;% 个体当前适应度     for i = 1:N        if  fx(i)  <fxm(i) fxm(i) = fx(i);     % 更新个体历史最佳适应度  xm(i,:) = x(i,:);   % 更新个体历史最佳位置(取值)  end   end  if   min(fxm)<  fym[fym, nmin] = min(fxm);   % 更新群体历史最佳适应度  ym = xm(nmin, :);      % 更新群体历史最佳位置  end  v = v * w + c1 * rand * (xm - x) + c2 * rand * (repmat(ym, N, 1) - x);% 速度更新  % 边界速度处理  v(v > vlimit(2)) = vlimit(2);  v(v < vlimit(1)) = vlimit(1);  x = x + v;% 位置更新  % 边界位置处理  x(x > limit(2)) = limit(2);  x(x < limit(1)) = limit(1);  record(iter) = fym;%最大值记录  subplot(1,2,1)mesh(X,Y,Z)hold on scatter3( x(:,1),x(:,2) ,f( x(:,1),x(:,2) ) ,'r*');title(['状态位置变化','-迭代次数：',num2str(iter)])subplot(1,2,2);plot(record);title('最优适应度进化过程')  pause(0.01)  iter = iter+1; end  figure(4);mesh(X,Y,Z); hold on 
scatter3( x(:,1),x(:,2) ,f( x(:,1),x(:,2) ) ,'r*');title('最终状态位置')  
disp(['最优值：',num2str(fym)]);  
disp(['变量取值：',num2str(ym)]);  

python代码

import numpy as np
import matplotlib.pyplot as plt
# 粒子（鸟）
class particle:def __init__(self):self.pos = 0  # 粒子当前位置self.speed = 0self.pbest = 0  # 粒子历史最好位置class PSO:def __init__(self):self.w = 0.5  # 惯性因子self.c1 = 1  # 自我认知学习因子self.c2 = 1  # 社会认知学习因子self.gbest = 0  # 种群当前最好位置self.N = 20  # 种群中粒子数量self.POP = []  # 种群self.iter_N = 100  # 迭代次数# 适应度值计算函数def fitness(self, x):return x + 16 * np.sin(5 * x) + 10 * np.cos(4 * x)# 找到全局最优解def g_best(self, pop):for bird in pop:if bird.fitness > self.fitness(self.gbest):self.gbest = bird.pos# 初始化种群def initPopulation(self, pop, N):for i in range(N):bird = particle()#初始化鸟bird.pos = np.random.uniform(-10, 10)#均匀分布bird.fitness = self.fitness(bird.pos)bird.pbest = bird.fitnesspop.append(bird)# 找到种群中的最优位置self.g_best(pop)# 更新速度和位置def update(self, pop):for bird in pop:# 速度更新speed = self.w * bird.speed + self.c1 * np.random.random() * (bird.pbest - bird.pos) + self.c2 * np.random.random() * (self.gbest - bird.pos)# 位置更新pos = bird.pos + speedif -10 < pos < 10: # 必须在搜索空间内bird.pos = posbird.speed = speed# 更新适应度bird.fitness = self.fitness(bird.pos)# 是否需要更新本粒子历史最好位置if bird.fitness > self.fitness(bird.pbest):bird.pbest = bird.pos# 最终执行def implement(self):# 初始化种群self.initPopulation(self.POP, self.N)# 迭代for i in range(self.iter_N):# 更新速度和位置self.update(self.POP)# 更新种群中最好位置self.g_best(self.POP)pso = PSO()
pso.implement()best_x=0
best_y=0
for ind in pso.POP:#print("x=", ind.pos, "f(x)=", ind.fitness)if ind.fitness>best_y:best_y=ind.fitnessbest_x=ind.pos
print(best_y)
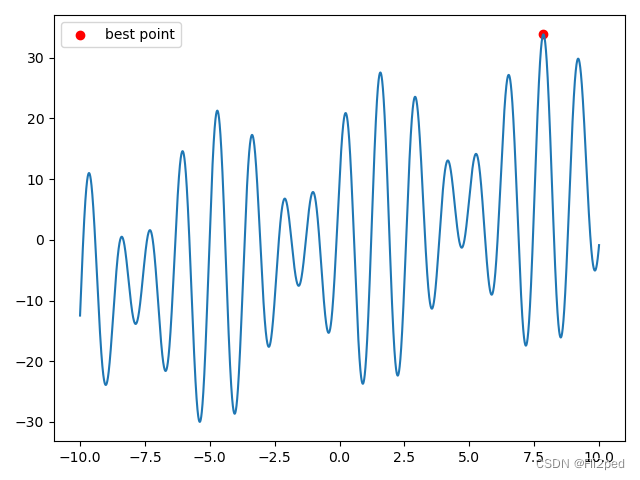
print(best_x)x = np.linspace(-10, 10, 100000)def fun(x):return x + 16 * np.sin(5 * x) + 10 * np.cos(4 * x)
y=fun(x)
plt.plot(x, y)plt.scatter(best_x,best_y,c='r',label='best point')
plt.legend()
plt.show()

注：
算法思想和matlab代码来自于
【通俗易懂讲算法-最优化之粒子群优化（PSO）】
python代码来自于
粒子群PSO优化算法学习笔记 及其python实现（附讲解如何使用python语言sko.PSO工具包）