贵阳学网站建设无代码免费web开发平台
目录
- 数据结构概述
- 逻辑结构
- 存储结构
- 算法概述
- 如何理解“大O记法”
- 时间复杂度
- 空间复杂度
数据结构概述
- 数据结构可以简单的理解为数据与数据之间所存在的一些关系,数据的结构分为数据的存储结构和数据的逻辑结构。
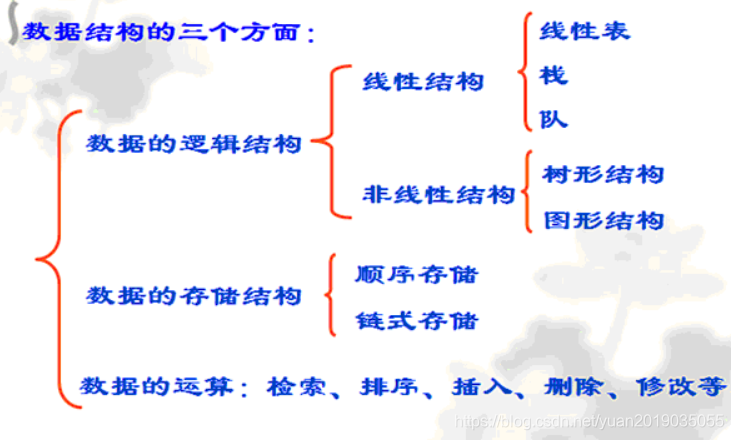
逻辑结构
- 集合结构:数据元素同属于一个集合,他们之间是并列关系,无其他的关系;可以理解为中学时期学习的集合,在一个范围之内,有很多的元素,元素间没有什么关系
- 线性结构:元素之间存在着一对一的关系;可以理解为每个学生对应着一个学号,学号与姓名就是线性结构
- 树形结构:元素之间存在着一对多的关系,可以简单理解为家庭族谱一样,一代接一代
- 图形结构:元素之间存在多对多的关系,每一个元素可能对应着多个元素,或被多个元素对应,网状图
存储结构
- 顺序存储结构:就是将数据进行连续的存储,我们可以将它比喻成学校食堂打饭排队一样,一个接着一个;
- 链式存储结构:不是按照顺序存储的,后一个进来的数只需要将他的地址告诉前一个节点,前一个节点中就存放了它后面那个数的地址,所以最后一个数的存储地址就是为null;可以将这种结构比喻成商场吃饭叫号,上面的号码比喻成是地址,你可以之后后面的地址是什么,上面的其他内容就是该节点的内容;
- 区别:
- 顺序存储的特点是查询快,插入或者删除慢
- 链式存储的特点是查询慢,插入或者删除快
算法概述
- 同一问题不同解决方法
- 通过时间和空间复杂度判断算法的优劣
- 算法没有最好的,只有最合适的,学习算法是为了积累学习思路,掌握学习思路,并不是为了解决某问题去记住某种算法;对于时间复杂度与空间复杂度,现在大多数开发情况下,我们都在使用以空间换时间,耗费更多的内存,来保证拥有更快的速度。
- 各排序算法复杂度及稳定性:
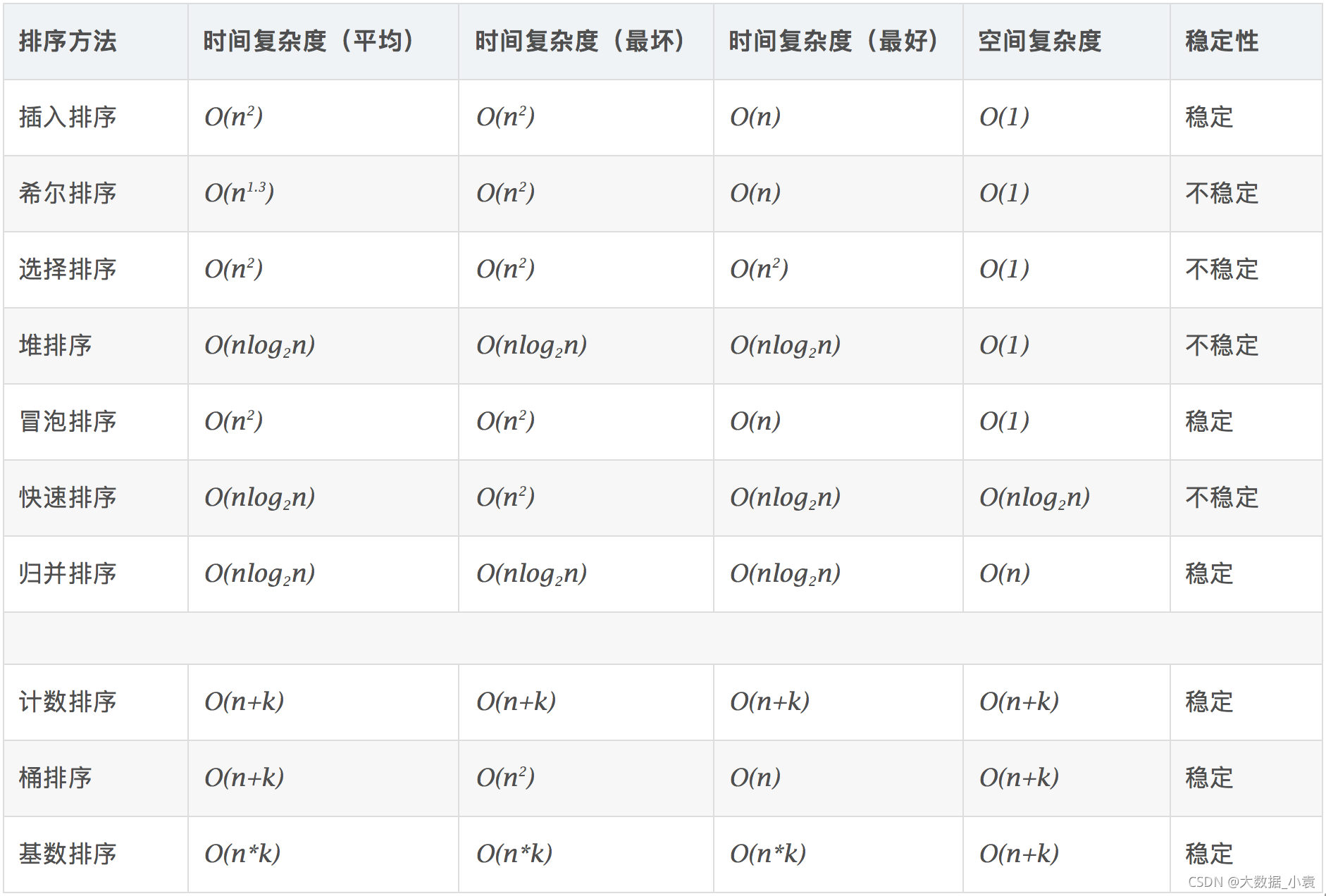
如何理解“大O记法”
对于算法进行特别具体的细致分析虽然很好,但在实践中的实际价值有限。对于算法的时间性质和空间性质,最重要的是其数量级和趋势,这些是分析算法效率的主要部分。而计量算法基本操作数量的规模函数中那些常量因子可以忽略不计。例如,可以认为 3n^2 和 100n^2 属于同一个量级,如果两个算法处理同样规模实例的代价分别为这两个函数,就认为它们的效率“差不多”,都为n^2级。
时间复杂度
一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。算法中的语句执行次数称为语句频度或时间频度,记为T(n)。n 称为问题的规模,当 n 不断变化时,时间频度T(n)也会不断变化。但有时我们想知道它变化时呈现什么规律。为此,我们引入时间复杂度概念。
一般情况下,算法中基本操作重复执行的次数是问题规模 n 的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当 n 趋近于无究大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n))为算法的渐进时间复杂度,简称时间复杂度。
有时候,算法中基本操作重复执行的次数还随问题的输入数据集不同而不同,如在冒泡排序中,输入数据有序而无序,结果是不一样的。此时,我们计算平均值。
时间复杂度基本计算规则:
- 基本操作,即只有常数项,认为其时间复杂度为O(1)
- 顺序结构,时间复杂度按加法进行计算
- 循环结构,时间复杂度按乘法进行计算
- 分支结构,时间复杂度取最大值
- 判断一个算法的效率时,往往只需要关注操作数量的最高次项,其它次要项和常数项可以忽略
- 在没有特殊说明时,我们所分析的算法的时间复杂度都是指最坏时间复杂度
常用时间复杂度:
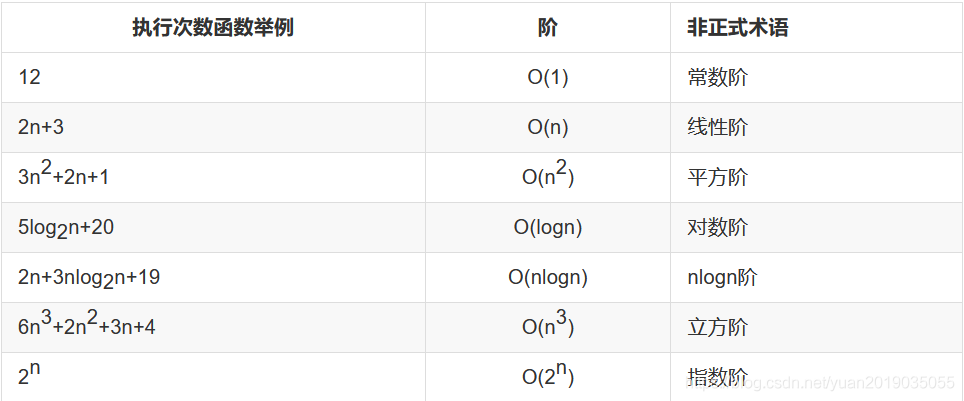
注意:经常将log2n(以2为底的对数)简写成logn
常见时间复杂度之间的关系:
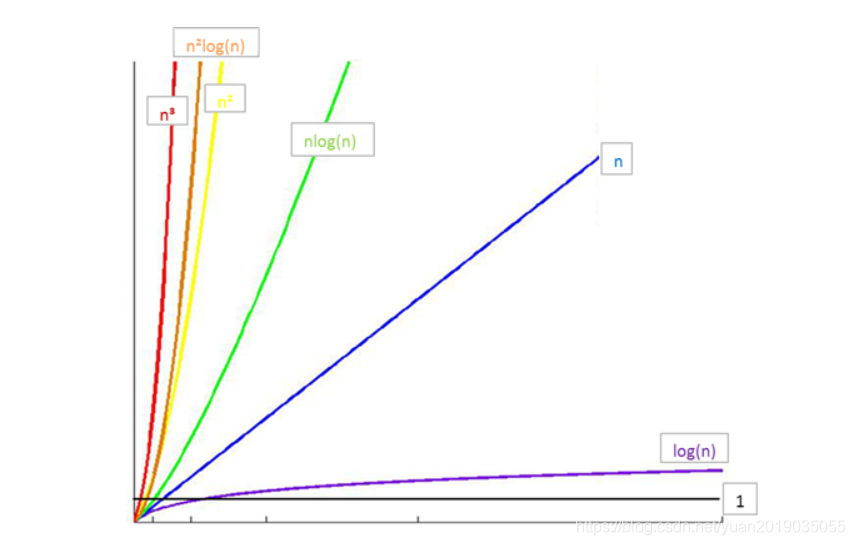
- 所以时间消耗由小到大为:
O(1) < O(log n) < O(n) < O(nlog n) < O(n^2) < O(2^n) < O(n!) < O(n^n)
案例1:
count = 0; (1)for(i = 0;i <= n;i++) (2)for(j = 0;j <= n;j++) (3)count++; (4)
- 语句(1)执行1次
- 语句(2)执行n次
- 语句(3)执行n^2次
- 语句(4)执行n^2次
- 时间复杂度为:
T(n) = 1+n+n^2+n^2 = O(n^2)
案例2:
a = 1; (1)
b = 2; (2)
for(int i = 1;i <= n;i++) { (3)int s = a + b; (4)b = a; (5)a = s; (6)
}
- 语句(1)、(2)执行1次
- 语句(3)执行n次
- 语句(4)、(5)、(6)执行n次
- 时间复杂度为:
T(n) = 1+1+4n = o(n)
案例3:
i = 1; (1)
while(i<n) {i = i*2; (2)
}
- 语句(1)的频度是1
- 设语句(2)的频度是
f(n),则2f(n)<=n;f(n)<=log2n,取最大值f(n) = log2n - 时间复杂度为:
T(n) = O(log2n)
空间复杂度
-
算法的空间复杂度计算公式:
S(n) = 0( f(n) ),其中 n 为输入规模,f(n)为语句关于 n 所占存储空间的函数 -
一个算法在计算机存储器上所占用的存储空间,包括三个方面
- 存储算法本身所占用的存储空间
- 算法的输入输出数据所占用的存储空间
- 算法在运行过程中临时占用的存储空间
案例:指定的数组进行反转,并返回反转的内容
解法一:
public static int[] reverse1(int[] arr) {int n = arr.length; //申请4个字节int temp; //申请4个字节for (int start = 0, end = n - 1; start <= end; start++, end--) {temp = arr[start];arr[start] = arr[end];arr[end] = temp;}return arr;
}
- 空间复杂度为:
S(n) = 4+4 = O(8) = O(1)
解法二:
public static int[] reverse2(int[] arr) {int n = arr.length; //申请4个字节int[] temp = new int[n]; //申请n*4个字节+数组自身头信息开销24个字节for (int i = n - 1; i >= 0; i--) {temp[n - 1 - i] = arr[i];}return temp;
}
- 空间复杂度为:
S(n) = 4+4n+24 = O(n+28) = O(n)
根据大O推导法则,算法一的空间复杂度为0(1),算法二的空间复杂度为0(n),所以从空间占用的角度讲,算法一要优于算法二。
由于java中有内存垃圾回收机制,并且jvm对程序的内存占用也有优化(例如即时编译) , 我们无法精确的评估一个java程序的内存占用情况,但是了解了java的基本内存占用,使我们可以对java程序的内存占用情况进行估算。
由于现在的计算机设备内存一般都比较大,基本上个人计算机都是4G起步,大的可以达到32G ,所以内存占用一般情况下并不是我们算法的瓶颈,普通情况下直接说复杂度,默认为算法的时间复杂度。
但是,如果你做的程序是嵌入式开发,尤其是一些传感器设备上的内置程序,由于这些设备的内存很小, 一般为几kb,这个时候对算法的空间复杂度就有要求了,但是一般做java开发的,基本上都是服务器开发, 一般不存在这样的问题。
