建设个人博客网站精准营销的案例
机器学习笔记之流形模型——标准流模型基本介绍
- 引言
- 回顾:隐变量模型的缺陷
- 标准流(Normalizing Flow\text{Normalizing Flow}Normalizing Flow)思想
- 分布变换的推导过程
引言
本节将介绍概率生成模型——标准流模型(Normalizing Flow\text{Normalizing Flow}Normalizing Flow)。
回顾:隐变量模型的缺陷
关于隐变量模型(Latent Variable Model,LVM\text{Latent Variable Model,LVM}Latent Variable Model,LVM),如果表示隐变量的随机变量集合Z\mathcal ZZ足够复杂的话,很容易出现积分难问题:
此时隐变量Z\mathcal ZZ的维度(随机变量个数)极高(M)(\mathcal M)(M),对Z\mathcal ZZ求解积分的代价是极大的(Intractable)(\text{Intractable})(Intractable).
P(X)⏟Intractable=∫ZP(Z,X)dZ=∫ZP(Z)⋅P(X∣Z)dZ=∫Z1⋯∫ZMP(Z1,⋯,ZM)⋅P(X∣Z1,⋯,ZM)dZ1,⋯,ZM\begin{aligned} \underbrace{\mathcal P(\mathcal X) }_{\text{Intractable}} & = \int_{\mathcal Z} \mathcal P(\mathcal Z,\mathcal X) d\mathcal Z \\ & = \int_{\mathcal Z} \mathcal P(\mathcal Z) \cdot \mathcal P(\mathcal X \mid \mathcal Z) d\mathcal Z \\ & = \int_{\mathcal Z_1} \cdots \int_{\mathcal Z_{\mathcal M}} \mathcal P(\mathcal Z_1,\cdots,\mathcal Z_{\mathcal M}) \cdot \mathcal P(\mathcal X \mid \mathcal Z_1,\cdots,\mathcal Z_{\mathcal M}) d\mathcal Z_1,\cdots,\mathcal Z_{\mathcal M} \end{aligned}IntractableP(X)=∫ZP(Z,X)dZ=∫ZP(Z)⋅P(X∣Z)dZ=∫Z1⋯∫ZMP(Z1,⋯,ZM)⋅P(X∣Z1,⋯,ZM)dZ1,⋯,ZM
从而,关于隐变量Z\mathcal ZZ的后验概率P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)P(Z∣X)也同样是极难求解的:
P(Z∣X)⏟Intractable=P(Z,X)P(X)=P(Z)⋅P(X∣Z)P(X)⏟Intractable\begin{aligned} \underbrace{\mathcal P(\mathcal Z \mid \mathcal X)}_{\text{Intractable}} & = \frac{\mathcal P(\mathcal Z,\mathcal X)}{\mathcal P(\mathcal X)} \\ & = \frac{\mathcal P(\mathcal Z) \cdot \mathcal P(\mathcal X \mid \mathcal Z)}{\underbrace{\mathcal P(\mathcal X)}_{\text{Intractable}}} \end{aligned}IntractableP(Z∣X)=P(X)P(Z,X)=IntractableP(X)P(Z)⋅P(X∣Z)
针对这种问题,由于无法得到精确解/精确解计算代价极高,因而通常采用近似推断(Approximate Inference\text{Approximate Inference}Approximate Inference)的方式对P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)P(Z∣X)近似求解。
例如变分自编码器(Variational Auto-Encoder,VAE\text{Variational Auto-Encoder,VAE}Variational Auto-Encoder,VAE),它的底层逻辑是使用重参数化技巧将人为设定分布Q(Z∣X)\mathcal Q(\mathcal Z \mid \mathcal X)Q(Z∣X)视作关于参数ϕ\phiϕ的函数Q(Z∣X,ϕ)\mathcal Q(\mathcal Z \mid \mathcal X,\phi)Q(Z∣X,ϕ),并通过神经网络学习参数ϕ\phiϕ并使其近似P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)P(Z∣X)。关于变分自编码器的模型结构表示如下:
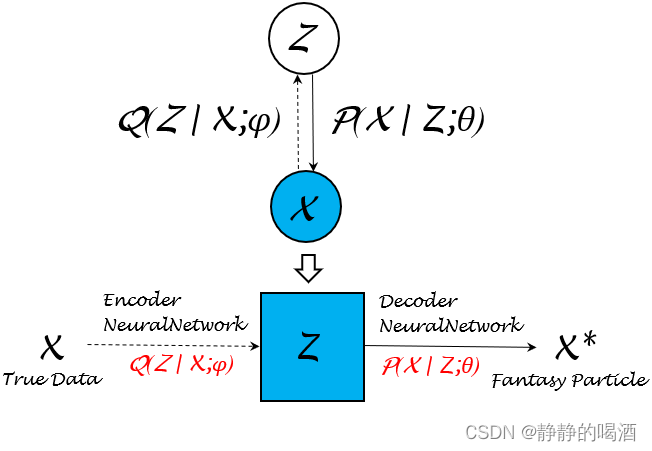
关于编码器(Encoder\text{Encoder}Encoder)函数Q(Z∣X;ϕ)\mathcal Q(\mathcal Z \mid \mathcal X;\phi)Q(Z∣X;ϕ)与解码器(Decoder\text{Decoder}Decoder)函数P(X∣Z;θ)\mathcal P(\mathcal X \mid \mathcal Z;\theta)P(X∣Z;θ),变分自编码器的目标函数表示如下:
一个有趣的现象:其中−KL[Q(Z∣X;ϕ)∣∣P(Z;θ(t))]- \text{KL} [\mathcal Q(\mathcal Z \mid \mathcal X;\phi) || \mathcal P(\mathcal Z ;\theta^{(t)})]−KL[Q(Z∣X;ϕ)∣∣P(Z;θ(t))]只是一个关于ϕ\phiϕ的惩罚项(约束),并且这个约束直接作用于EQ(Z∣X;ϕ)[logP(X∣Z;θ)]\mathbb E_{\mathcal Q(\mathcal Z \mid \mathcal X;\phi)} \left[\log \mathcal P(\mathcal X \mid \mathcal Z;\theta)\right]EQ(Z∣X;ϕ)[logP(X∣Z;θ)].因此真正迭代的只有参数θ(θ(t)⇒θ(t+1))\theta(\theta^{(t)}\Rightarrow \theta^{(t+1)})θ(θ(t)⇒θ(t+1)),参数ϕ\phiϕ仅是迭代过程中伴随着θ\thetaθ的更新而更新。
{L(ϕ,θ,θ(t))=EQ(Z∣X;ϕ)[logP(X∣Z;θ)]−KL[Q(Z∣X;ϕ)∣∣P(Z;θ(t))](θ^(t+1),ϕ^(t+1))=argmaxθ,ϕL(ϕ,θ,θ(t))\begin{cases} \mathcal L(\phi,\theta,\theta^{(t)}) = \mathbb E_{\mathcal Q(\mathcal Z \mid \mathcal X;\phi)} \left[\log \mathcal P(\mathcal X \mid \mathcal Z;\theta)\right] - \text{KL} [\mathcal Q(\mathcal Z \mid \mathcal X;\phi) || \mathcal P(\mathcal Z;\theta^{(t)})] \\ \quad \\ (\hat {\theta}^{(t+1)},\hat {\phi}^{(t+1)}) = \mathop{\arg\max}\limits_{\theta,\phi} \mathcal L(\phi,\theta,\theta^{(t)}) \end{cases}⎩⎨⎧L(ϕ,θ,θ(t))=EQ(Z∣X;ϕ)[logP(X∣Z;θ)]−KL[Q(Z∣X;ϕ)∣∣P(Z;θ(t))](θ^(t+1),ϕ^(t+1))=θ,ϕargmaxL(ϕ,θ,θ(t))
关于目标函数L(ϕ,θ,θ(t))\mathcal L(\phi,\theta,\theta^{(t)})L(ϕ,θ,θ(t))的底层逻辑是最大化ELBO\text{ELBO}ELBO:
(θ^(t+1),ϕ^(t+1))=argmaxθ,ϕ{EQ(Z∣X;ϕ)[logP(X,Z;θ)Q(Z∣X;ϕ)]}(\hat {\theta}^{(t+1)},\hat {\phi}^{(t+1)}) = \mathop{\arg\max}\limits_{\theta,\phi} \left\{\mathbb E_{\mathcal Q(\mathcal Z \mid \mathcal X;\phi)} \left[\log \frac{\mathcal P(\mathcal X,\mathcal Z;\theta)}{\mathcal Q(\mathcal Z \mid \mathcal X;\phi)}\right]\right\}(θ^(t+1),ϕ^(t+1))=θ,ϕargmax{EQ(Z∣X;ϕ)[logQ(Z∣X;ϕ)P(X,Z;θ)]}
也就是说,它仅仅是最大化了极大似然估计logP(X;θ)\log \mathcal P(\mathcal X;\theta)logP(X;θ)的下界。实际上,它并没有直接对对数似然函数求解最优化问题。
这不可避免地存在误差,毕竟最优化对数似然函数和最优化它的下界 是两个概念。这一切的核心问题均在于P(X)\mathcal P(\mathcal X)P(X)无法得到精确解。
如果存在一种模型,它在学习任务过程中,P(X)\mathcal P(\mathcal X)P(X)是可求解的(tractable\text{tractable}tractable),自然不会出现上述一系列的近似操作了。
标准流(Normalizing Flow\text{Normalizing Flow}Normalizing Flow)思想
关于样本X\mathcal XX的概率分布P(X)\mathcal P(\mathcal X)P(X),它可能是复杂的。但流模型(Flow-based Model\text{Flow-based Model}Flow-based Model)的思想是:分布P(X)\mathcal P(\mathcal X)P(X)的复杂并不是一蹴而就的,而是通过若干次的变化而产生出的复杂结果。
关于流模型的概率图结构可表示为如下形式:
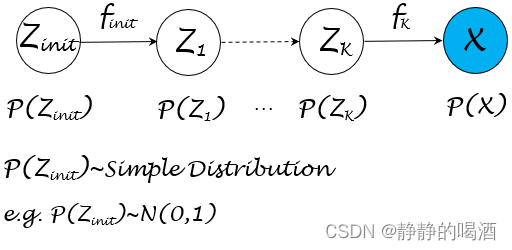
从模型结构中可以观察到,既然分布P(X)\mathcal P(\mathcal X)P(X)比较复杂,那么可以构建隐变量Z\mathcal ZZ与X\mathcal XX之间的函数关系X=f(Z)\mathcal X = f(\mathcal Z)X=f(Z),从而通过换元的方式描述P(Z)\mathcal P(\mathcal Z)P(Z)与P(X)\mathcal P(\mathcal X)P(X)的函数关系。
如果隐变量Z\mathcal ZZ的结构同样复杂,可以继续针对该隐变量创造新的隐变量并构建函数关系。以此类推,最终可以通过一组服从简单分布的随机变量Zinit\mathcal Z_{init}Zinit通过若干次的函数的嵌套表示,得到关于X\mathcal XX的关联关系,从而得到Pinit(Zinit)⇒P(X)\mathcal P_{init}(\mathcal Z_{init}) \Rightarrow \mathcal P(\mathcal X)Pinit(Zinit)⇒P(X)的函数关系。
分布变换的推导过程
以上图中隐变量ZK\mathcal Z_{\mathcal K}ZK和观测变量X\mathcal XX之间关联关系示例:
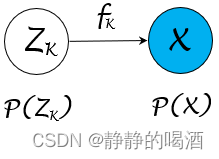
- 创建假设:fKf_{\mathcal K}fK是一个 连续、可逆 函数,满足X=fK(ZK)\mathcal X = f_{\mathcal K}(\mathcal Z_{\mathcal K})X=fK(ZK)。其中ZK,X\mathcal Z_{\mathcal K},\mathcal XZK,X均表示随机变量集合,并服从对应的概率分布:
其中PX(X)\mathcal P_{\mathcal X}(\mathcal X)PX(X)表示关于X\mathcal XX的概率分布,并且变量是X.ZK\mathcal X.\mathcal Z_{\mathcal K}X.ZK对应分布同理。反过来,由于fKf_{\mathcal K}fK函数可逆,因而有:ZK=fK−1(X)\mathcal Z_{\mathcal K} = f_{\mathcal K}^{-1}(\mathcal X)ZK=fK−1(X).
ZK∼PZK(ZK),X∼PX(X);ZK,X∈Rp\mathcal Z_{\mathcal K} \sim \mathcal P_{\mathcal Z_{\mathcal K}}(\mathcal Z_{\mathcal K}),\mathcal X \sim \mathcal P_{\mathcal X}(\mathcal X);\quad \mathcal Z_{\mathcal K},\mathcal X \in \mathbb R^pZK∼PZK(ZK),X∼PX(X);ZK,X∈Rp
- 不可否认的是,无论是PZK(ZK)\mathcal P_{\mathcal Z_{\mathcal K}}(\mathcal Z_{\mathcal K})PZK(ZK)还是PX(X)\mathcal P_{\mathcal X}(\mathcal X)PX(X),它们都是概率分布。根据概率密度积分的定义,必然有:
∫ZKPZK(ZK)dZK=∫XPX(X)dX=1\int_{\mathcal Z_{\mathcal K}} \mathcal P_{\mathcal Z_{\mathcal K}}(\mathcal Z_{\mathcal K}) d\mathcal Z_{\mathcal K} = \int_{\mathcal X} \mathcal P_{\mathcal X}(\mathcal X) d\mathcal X =1∫ZKPZK(ZK)dZK=∫XPX(X)dX=1
从而有:
在变分推断——重参数化技巧一节中也使用这种描述进行换元,在不定积分中,PZK(ZK)dZK\mathcal P_{\mathcal Z_{\mathcal K}}(\mathcal Z_{\mathcal K}) d\mathcal Z_{\mathcal K}PZK(ZK)dZK和PX(X)dX\mathcal P_{\mathcal X}(\mathcal X)d \mathcal XPX(X)dX必然相等;但是在定积分中,ZK,X\mathcal Z_{\mathcal K},\mathcal XZK,X位于不同的特征空间,对应的积分值(有正有负)存在差异。因此需要加上‘模’符号。
∣PZK(ZK)dZK∣=∣PX(X)dX∣|\mathcal P_{\mathcal Z_{\mathcal K}}(\mathcal Z_{\mathcal K}) d\mathcal Z_{\mathcal K}| = |P_{\mathcal X}(\mathcal X) d\mathcal X|∣PZK(ZK)dZK∣=∣PX(X)dX∣
但由于PZK(ZK),PX(X)\mathcal P_{\mathcal Z_{\mathcal K}}(\mathcal Z_{\mathcal K}),\mathcal P_{\mathcal X}(\mathcal X)PZK(ZK),PX(X)它们是概率密度函数,它们的实际结果表示概率值(恒正)。因此∣PX(X)∣=PX(X)|\mathcal P_{\mathcal X}(\mathcal X)| = \mathcal P_{\mathcal X}(\mathcal X)∣PX(X)∣=PX(X),PZK(ZK)\mathcal P_{\mathcal Z_{\mathcal K}}(\mathcal Z_{\mathcal K})PZK(ZK)同理。经过移项,可将概率分布之间的关系表示为如下形式:
PX(X)=∣dZKdX∣⋅PZK(ZK)\mathcal P_{\mathcal X}(\mathcal X) = \left|\frac{d\mathcal Z_{\mathcal K}}{d\mathcal X}\right| \cdot \mathcal P_{\mathcal Z_{\mathcal K}}(\mathcal Z_{\mathcal K})PX(X)=dXdZK⋅PZK(ZK)
将ZK=fK−1(X)\mathcal Z_{\mathcal K} = f_{\mathcal K}^{-1}(\mathcal X)ZK=fK−1(X)代入,最终可得到如下形式:
PX(X)=∣∂fK−1(X)∂X∣⋅PZK(ZK)\mathcal P_{\mathcal X}(\mathcal X) = \left|\frac{\partial f_{\mathcal K}^{-1}(\mathcal X)}{\partial \mathcal X}\right| \cdot \mathcal P_{\mathcal Z_{\mathcal K}}(\mathcal Z_{\mathcal K})PX(X)=∂X∂fK−1(X)⋅PZK(ZK) - 观察系数项∣∂fK−1(X)∂X∣\left|\frac{\partial f_{\mathcal K}^{-1}(\mathcal X)}{\partial \mathcal X}\right|∂X∂fK−1(X),它是一个标量、常数,但∂fK−1(X)∂X\frac{\partial f_{\mathcal K}^{-1}(\mathcal X)}{\partial\mathcal X}∂X∂fK−1(X)自身是一个矩阵:
该矩阵被称作雅可比矩阵Jacobian\text{Jacobian}Jacobian
∂fK−1(X)∂X=[∂fK−1(X1)∂X1∂fK−1(X1)∂X2⋯∂fK−1(X1)∂Xp∂fK−1(X2)∂X1∂fK−1(X2)∂X2⋯∂fK−1(X2)∂Xp⋮⋮⋱⋮∂fK−1(Xp)∂X1∂fK−1(Xp)∂X2⋯∂fK−1(Xp)∂Xp]p×p\frac{\partial f_{\mathcal K}^{-1}(\mathcal X)}{\partial \mathcal X} = \begin{bmatrix} \frac{\partial f_{\mathcal K}^{-1}(\mathcal X_1)}{\partial \mathcal X_1} & \frac{\partial f_{\mathcal K}^{-1}(\mathcal X_1)}{\partial \mathcal X_2}& \cdots & \frac{\partial f_{\mathcal K}^{-1}(\mathcal X_1)}{\partial \mathcal X_p} \\ \frac{\partial f_{\mathcal K}^{-1}(\mathcal X_2)}{\partial \mathcal X_1} & \frac{\partial f_{\mathcal K}^{-1}(\mathcal X_2)}{\partial \mathcal X_2} & \cdots & \frac{\partial f_{\mathcal K}^{-1}(\mathcal X_2)}{\partial \mathcal X_p}\\ \vdots & \vdots & \ddots & \vdots\\ \frac{\partial f_{\mathcal K}^{-1}(\mathcal X_p)}{\partial \mathcal X_1} & \frac{\partial f_{\mathcal K}^{-1}(\mathcal X_p)}{\partial \mathcal X_2} & \cdots & \frac{\partial f_{\mathcal K}^{-1}(\mathcal X_p)}{\partial \mathcal X_p} \end{bmatrix}_{p \times p}∂X∂fK−1(X)=∂X1∂fK−1(X1)∂X1∂fK−1(X2)⋮∂X1∂fK−1(Xp)∂X2∂fK−1(X1)∂X2∂fK−1(X2)⋮∂X2∂fK−1(Xp)⋯⋯⋱⋯∂Xp∂fK−1(X1)∂Xp∂fK−1(X2)⋮∂Xp∂fK−1(Xp)p×p
那么∣∂fK−1(X)∂X∣\left|\frac{\partial f_{\mathcal K}^{-1}(\mathcal X)}{\partial \mathcal X}\right|∂X∂fK−1(X)实际上是与雅克比矩阵对应的雅克比行列式(Jacobian Determinant\text{Jacobian Determinant}Jacobian Determinant)的绝对值。使用det[∂fK−1(X)∂X]\text{det}\left[\frac{\partial f_{\mathcal K}^{-1}(\mathcal X)}{\partial \mathcal X}\right]det[∂X∂fK−1(X)]进行表示:
PX(X)=∣det[∂fK−1(X)∂X]∣⋅PZK(ZK)\mathcal P_{\mathcal X}(\mathcal X) = \left|\text{det}\left[\frac{\partial f_{\mathcal K}^{-1}(\mathcal X)}{\partial \mathcal X}\right]\right| \cdot \mathcal P_{\mathcal Z_{\mathcal K}}(\mathcal Z_{\mathcal K})PX(X)=det[∂X∂fK−1(X)]⋅PZK(ZK) - 继续变换,观察∂fK−1(X)∂X\frac{\partial f_{\mathcal K}^{-1}(\mathcal X)}{\partial \mathcal X}∂X∂fK−1(X),可以继续向下变换:
{∂fK−1(X)∂X⋅∂fK(ZK)∂ZK=1⇒∂fK−1(X)∂X=[∂fK(ZK)∂ZK]−1⇒∣det[∂fK−1(X)∂X]∣=∣det[∂fK(ZK)∂ZK]∣−1\begin{cases} \frac{\partial f_{\mathcal K}^{-1}(\mathcal X)}{\partial \mathcal X} \cdot \frac{\partial f_{\mathcal K}(\mathcal Z_{\mathcal K})}{\partial \mathcal Z_{\mathcal K}} = 1 \Rightarrow \frac{\partial f_{\mathcal K}^{-1}(\mathcal X)}{\partial \mathcal X} = \left[\frac{\partial f_{\mathcal K}(\mathcal Z_{\mathcal K})}{\partial \mathcal Z_{\mathcal K}}\right]^{-1} \\ \Rightarrow \left|\text{det}\left[\frac{\partial f_{\mathcal K}^{-1}(\mathcal X)}{\partial \mathcal X}\right]\right| = \left|\text{det}\left[\frac{\partial f_{\mathcal K}(\mathcal Z_{\mathcal K})}{\partial \mathcal Z_{\mathcal K}}\right]\right|^{-1} \end{cases}⎩⎨⎧∂X∂fK−1(X)⋅∂ZK∂fK(ZK)=1⇒∂X∂fK−1(X)=[∂ZK∂fK(ZK)]−1⇒det[∂X∂fK−1(X)]=det[∂ZK∂fK(ZK)]−1
最终,分布PX(X)\mathcal P_{\mathcal X}(\mathcal X)PX(X)与分布PZK(ZK)\mathcal P_{\mathcal Z_{\mathcal K}}(\mathcal Z_{\mathcal K})PZK(ZK)之间的关系表示为:
PX(X)=∣det[∂fK(ZK)∂ZK]∣−1⋅PZK(ZK)\mathcal P_{\mathcal X}(\mathcal X) = \left|\text{det}\left[\frac{\partial f_{\mathcal K}(\mathcal Z_{\mathcal K})}{\partial \mathcal Z_{\mathcal K}}\right]\right|^{-1} \cdot \mathcal P_{\mathcal Z_{\mathcal K}}(\mathcal Z_{\mathcal K})PX(X)=det[∂ZK∂fK(ZK)]−1⋅PZK(ZK)
至此,从随机变量ZK\mathcal Z_{\mathcal K}ZK与随机变量X\mathcal XX之间的函数关系,转化为概率分布PX(X)\mathcal P_{\mathcal X}(\mathcal X)PX(X)与PZK(ZK)\mathcal P_{\mathcal Z_{\mathcal K}}(\mathcal Z_{\mathcal K})PZK(ZK)之间的函数关系已表示出来。而流模型中的每一个过程均是基于上述关系,一层一层计算过来。
不同于以往对P(X)\mathcal P(\mathcal X)P(X)的求解过程,它能够将P(X)\mathcal P(\mathcal X)P(X)描述出来,直到使用隐变量的层数选择完成,其对应的P(X)\mathcal P(\mathcal X)P(X)计算精度达到条件即可。关于流模型的学习方式依然是极大似然估计(Maximum Likelihood Estimation,MLE\text{Maximum Likelihood Estimation,MLE}Maximum Likelihood Estimation,MLE):
logPX(X)=log{∏k=1K∣det[∂fk(Zk)∂Zk]∣−1⋅Pinit(Zinit)}=logPinit(Zinit)+∑k=1Klog{∣det[∂fk(Zk)∂Zk]∣−1}\begin{aligned} \log \mathcal P_{\mathcal X}(\mathcal X) & = \log \left\{\prod_{k=1}^{\mathcal K} \left|\text{det} \left[\frac{\partial f_{k}(\mathcal Z_k)}{\partial \mathcal Z_k}\right]\right|^{-1} \cdot \mathcal P_{init}(\mathcal Z_{init})\right\} \\ & = \log \mathcal P_{init}(\mathcal Z_{init}) + \sum_{k=1}^{\mathcal K} \log \left\{\left|\text{det} \left[\frac{\partial f_{k}(\mathcal Z_k)}{\partial \mathcal Z_k}\right]\right|^{-1}\right\} \end{aligned}logPX(X)=log{k=1∏Kdet[∂Zk∂fk(Zk)]−1⋅Pinit(Zinit)}=logPinit(Zinit)+k=1∑Klog{det[∂Zk∂fk(Zk)]−1}
相关参考:
雅可比矩阵——百度百科
【机器学习白板推导系列(三十三) ~ 流模型(Flow Based Model)】
