当前位置：首页 > news >正文

国际业务网站有哪些网络广告代理

news 2025/7/8 20:48:08

国际业务网站有哪些,网络广告代理,未来十年电商前景如何,公司网站优化目录二叉搜索树二叉搜索树的简介： 二叉搜索树的查找： 二叉搜索树的效率： AVL树 AVL 树的简介： AVL 树的实现： AVL树的旋转右单旋左单旋左右双旋右左双旋完整 AVL树插入代码验证 AVL 树 AVL 树的性…

二叉搜索树

二叉搜索树的简介：

二叉搜索树的查找：

二叉搜索树的效率：

AVL树

AVL 树的简介：

AVL 树的实现：

AVL树的旋转

右单旋

左单旋

左右双旋

右左双旋

完整 AVL树插入代码

验证 AVL 树

AVL 树的性能

二叉搜索树

要想了解关于二叉平衡树的相关知识，了解二叉搜索树的相关概念是其前提！

二叉搜索树的简介：

特点：

结点的左子树上所有节点的值都小于该结点的值
结点的右子树上所有结点的值都大于该结点的值
左右子树也都是二叉搜索树

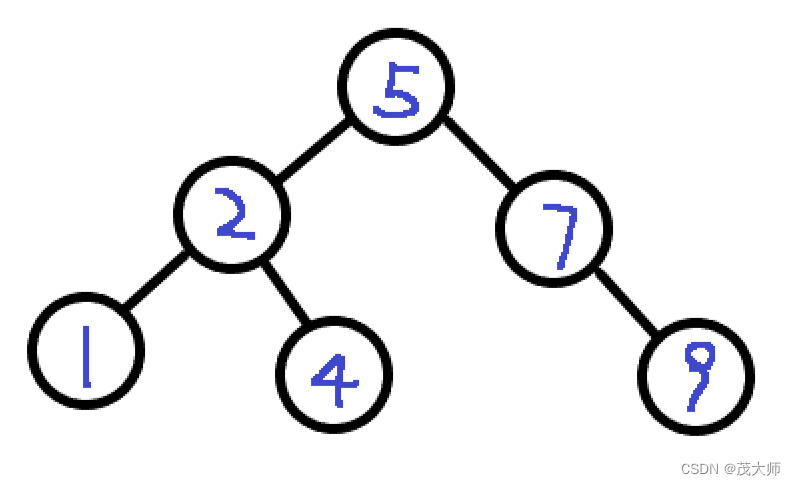
例图如下：

特性：

二叉搜索树最左侧节点为最小的节点，最右侧节点为最大的节点
采用中序遍历遍历二叉搜索树，能得到一个有序的序列

二叉搜索树的查找：

当根节点为空时，则返回 false
当根节点的值等于查询值，则返回 ture
当根节点的值小于查询值，则向其左子树进行查找
当根节点的值大于查询值，则向其右子树进行查找

例图如下：

当我们要查询 9 时，其二叉搜索树的查询过程如下：

先由根节点 5 开始，比较其值与查询值，发现 5 < 9 进而查询其右子树

到其右子树根节点，比较其值与查询值，发现 7 < 9 进而查询其右子树

到其右子树根节点，比较其值与查询值，发现 9 = 9，查询完毕返回 ture

二叉搜索树的效率：

二叉搜索树的平均查找长度与其节点的深度有关，节点越深，则比较次数越多！

上文例图中我们对数值 9 进行查询，进行了3次比较

下面的例图：同样为6个节点，同样是对9进行查询

根据上文二叉搜索树的查找方式，我们会发现其进行了 6 次比较

显然节点的插入次序不同，得到的二叉搜索树也会不同，导致当对同样的数值进行查找时，其效率也会有较大相差

最优情况：

该二叉搜索树树为二叉完全树，平均的比较次数为：log2N

最坏情况：

该二叉搜索树树为单枝树，平均的比较次数为：N/2

AVL树

当想避免二叉搜索树最坏情况出现时，AVL 树便是优化后的二叉搜索树！

AVL 树的简介：

特点：

结点的左子树上所有节点的值都小于该结点的值
结点的右子树上所有结点的值都大于该结点的值
其左右子树的高度差（平衡因子）的绝对值不超过 1
左右子树也都是 AVL 树

例图如下：

优点：

可以有效的降低树的高度，不会出现像单枝树这样的极端情况，有效的减少平均查找次数

AVL 树的实现：

1. 定义 AVL 树：

首先我们创建一个 TreeNode 静态类，将 AVL 树的相关属性定义完成

public class AVLTree {static class TreeNode {public int val;public int bf;//平衡因子 这里的平衡因子我们是 右子树高度-左子树高度public TreeNode left;//左孩子的引用public TreeNode right;//右孩子的引用 public TreeNode parent;//父亲节点的引用 //        构造方法public TreeNode(int val) {this.val=val;}}public TreeNode root;//根节点
}

2. 插入新结点：

第一步：先按照二叉搜索树插入结点方式进行新结点的插入

    public boolean insert(int val) {
//        根据传来的参数，创建一个新结点TreeNode node = new TreeNode(val);
//        判断根结点是否为空,为空则代表 AVL 树为空,直接将新插入的结点作为根结点即可if(root == null ){root = node;return true;}
//        创建一个 cur 结点,利用该结点去遍历这个树的结点TreeNode cur = root;//创建一个 parent 结点,该结点记录 cur 的父亲结点TreeNode parent = null;
//        创建该循环的目的是为了根据新增结点的值，来找到属于它应该插入的位置,当 cur == null 时，退出循环 且 parent 为新插入结点的父亲结点while (cur != null){if(cur.val > val) {
//                如果 cur 所指向的结点的值大于新增加结点的值，则向左寻找parent = cur;cur = cur.left;}else if (cur.val == val) {
//                新插入结点的值与 cur 所指向的结点的值相等,表示 AVL 树已有一个值与之相等的结点,因为 AVL 树中每个结点的值必须是唯一的,从而不必再插入一个重复值的结点return false;}else { 
//                如果 cur 所指向的节点的值小于新增加结点的值，则向右寻找parent = cur;cur = cur.right;}}
//        走到这说明 cur == null,意思是已经找到了新结点需要插入的位置,且 parent 结点已经记录到了 新结点的父亲结点 的位置if (parent.val > val){parent.left = node;}else {parent.right = node;}return true;}

第二步：根据插入结点后平衡因子的变化，对该树进行相应的调整，维持平衡因子的绝对值为 1

情况一：parent 结点平衡因子的绝对值为 0，该树无需调整

情况二：parent 结点平衡因子的绝对值为 1，该树不一定平衡，需向上继续查看结点，检查其平衡因子的绝对值

情况三：parent 结点平衡因子的绝对值为 2，该树一定不平衡，根据实际情况，对该树进行相应调整

结合上述三种情况我们可以先写出代码的大致框架，至于如何对树进行调整则有好几种情况

    public boolean insert(int val) {TreeNode node = new TreeNode(val);if(root == null ){root = node;return true;}TreeNode cur = root;TreeNode parent = null;while (cur != null){if(cur.val > val) {parent = cur;cur = cur.left;}else if (cur.val == val) {return false;}else {parent = cur;cur = cur.right;}}if (parent.val > val){parent.left = node;}else {parent.right = node;}//        这里定义一下新结点的父亲结点为 parentnode.parent = parent;
//        因为上段代码 cur == null，所以指定一下 cur 指向 node 结点，好为后面平衡因子的调整做准备cur = node;//        根据平衡因子进行树的调整
//        当 parent == null 时，说明 parent 已经爬到该树的根节点之上了，也就是调整完该树了while (parent != null) {if (cur == parent.right) {
//                新增结点在右树parent.bf++;}else {
//                新增结点在左树parent.bf--;}
//          在这里检查 parent 结点平衡因子绝对值的值if(parent.bf == 0) {
//            这里说明已经平衡了，无需调整}else if(parent.bf == 1 || parent.bf == -1) {
//            虽然 parent 结点是平衡的，但是还需向上查看结点，因为有可能不平cur = parent;parent = cur.parent;}else {
//            这里说明 parent 的平衡因子的绝对值为 2 了,该树必不平衡if (parent.bf == 2) {if (cur.bf == 1) {}else {
//                    这里是 cur.bf == -1}}else {
//                这里是 parent.bf == -2if (cur.bf == -1) {}else {
//                    这里是 cur.bf == 1}}}  } return true;}

AVL树的旋转

右单旋

具体解析：

5结点为新插入结点

代码：

看图理解代码相应含义

private void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;parent.left = subLR;subL.right = parent;subLR.parent = parent;parent.parent = subL;}

当然上述仅是 60结点作为根结点的情况，还有 60结点不为根结点的情况也许考虑到

更新代码：

private void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;parent.left = subLR;subL.right = parent;subLR.parent = parent;
//        这里必须先记录下 parent 的父亲结点TreeNode pParent = parent.parent;parent.parent = subL;
//        检查 parent 是否为根结点if(parent == root) {root = subL;root.parent = null;}else {
//            此时parent 是都父亲节点的，从而需要判断 parent是左子树的还是右子树的if(pParent.left == parent) {pParent.left = subL;}else {pParent.right = subL;}subL.parent = pParent;}}

当然右单旋完树之后还需要，调节其他结点的平衡因子

更新代码：

private void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;parent.left = subLR;subL.right = parent;subLR.parent = parent;
//        这里必须先记录下 parent 的父亲结点TreeNode pParent = parent.parent;parent.parent = subL;
//        检查 parent 是否为根结点if(parent == root) {root = subL;root.parent = null;}else {
//            此时parent 是都父亲节点的，从而需要判断 parent是左子树的还是右子树的if(pParent.left == parent) {pParent.left = subL;}else {pParent.right = subL;}subL.parent = pParent;}
//        更新上图两个结点的平衡因子subL.bf = 0;parent.bf = 0;}

当然我们上述思路中，还有一个问题没有考虑到，就是 subLR 可能为空

最终代码：

此代码为完整右单旋逻辑代码

private void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;parent.left = subLR;subL.right = parent;
//        如果 subLR 不为 null，我们才执行，该行代码if(subLR != null){subLR.parent = parent;}
//        这里必须先记录下 parent 的父亲结点TreeNode pParent = parent.parent;parent.parent = subL;
//        检查 parent 是否为根结点if(parent == root) {root = subL;root.parent = null;}else {
//            此时parent 是都父亲节点的，从而需要判断 parent是左子树的还是右子树的if(pParent.left == parent) {pParent.left = subL;}else {pParent.right = subL;}subL.parent = pParent;}
//        更新上图两个结点的平衡因子subL.bf = 0;parent.bf = 0;}

左单旋

代码上左单旋和右单旋逻辑上是一样的，可参照着右单旋代码写

最终代码：

此代码为完整左单旋逻辑代码

private void rotateLeft(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;parent.right = subRL;subR.left = parent;if(subRL != null) {subRL.parent = parent;}TreeNode pParent = parent.parent;parent.parent = subR;if (root == parent) {root = subR;root.parent = null;}else {if (pParent.left == parent){pParent.left = subR;}else {pParent.right = subR;}subR.parent = pParent;}subR.bf = 0;parent.bf = 0;}

左右双旋

代码：

看图理解代码相应含义

    private void rotateLR(TreeNode parent) {
//        先左旋后右旋rortateLeft(parent.left);rortateRight(parent);}

当然左右双旋完树之后还需要，调节其他结点的平衡因子

最终代码：

此代码为完整左右双旋逻辑代码

private void rotateLR(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;int bf = subLR.bf;
//        先左旋后右旋rotateLeft(parent.left);rotateRight(parent);
//        明确一点，当 bf 为 0 时，本身就是平衡的，无需再修改平衡因子if(bf == -1){subL.bf = 0;subLR.bf = 0;parent.bf = 1;}else if(bf == 1){subL.bf = -1;subLR.bf = 0;parent.bf = 0;}}

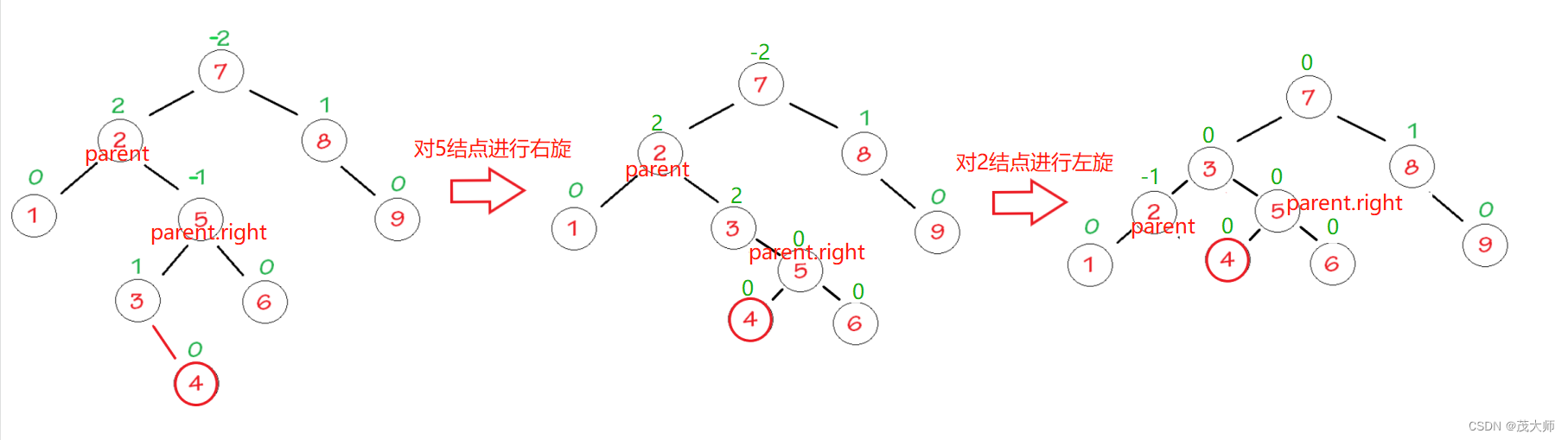
右左双旋

最终代码：

此代码为完整左右双旋逻辑代码

private void rotateRL(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;int bf = subRL.bf;rotateRight(parent.right);rotateLeft(parent);if(bf == -1){parent.bf = -1;subR.bf = 0;subRL.bf = 0;}else if(bf == 1){parent.bf = 0;subR.bf = 1;subRL.bf = 0;}}

完整 AVL树插入代码

我们将这四种旋转填入到相对应的位置

public boolean insert(int val) {//根据传来的参数，创建一个新结点TreeNode node = new TreeNode(val);
//        判断根结点是否为空,为空则代表 AVL 树为空,直接将新插入的结点作为根结点即可if(root == null ){root = node;return true;}
//        创建一个 cur 结点,利用该结点去遍历这个树的结点TreeNode cur = root;//创建一个 parent 结点,该结点记录 cur 的父亲结点TreeNode parent = null;
//        创建该循环的目的是为了根据新增结点的值，来找到属于它应该插入的位置,当 cur == null 时，退出循环 且 parent 为新插入结点的父亲结点while (cur != null){if(cur.val > val) {
//                如果 cur 所指向的结点的值大于新增加结点的值，则向左寻找parent = cur;cur = cur.left;}else if (cur.val == val) {
//                新插入结点的值与 cur 所指向的结点相等,表示 AVL 树已有一个值与之相等的结点,因为 AVL 树中每个结点的值必须是唯一的,从而不必再插入一个重复值的结点return false;}else {
//                如果 cur 所指向的节点的值小于新增加结点的值，则向右寻找parent = cur;cur = cur.right;}}
//        走到这说明 cur == null,意思是已经找到了新结点需要插入的位置,且 parent 结点已经记录到了 新结点的父亲结点 的位置if (parent.val > val){parent.left = node;}else {parent.right = node;}//        这里定义一下新结点的父亲结点为 parentnode.parent = parent;
//        因为上段代码 cur == null，所以指定一下 cur 指向 node 结点，好为后面平衡因子的调整做准备cur = node;//        根据平衡因子进行树的调整
//        当 parent == null 时，说明 parent 已经爬到该树的根节点之上了，也就是调整完该树了while (parent != null) {if (cur == parent.right) {
//                新增结点在右树parent.bf++;}else {
//                新增结点在左树parent.bf--;}
//          在这里检查 parent 结点平衡因子绝对值的值if(parent.bf == 0) {
//            这里说明已经平衡了，无需调整}else if(parent.bf == 1 || parent.bf == -1) {
//            虽然 parent 结点是平衡的，但是还需向上查看结点，因为有可能不平cur = parent;parent = cur.parent;}else {
//            这里说明 parent 的平衡因子的绝对值为 2 了,该树必不平衡if (parent.bf == 2) {if (cur.bf == 1) {
//                        这里进行左旋rotateLeft(parent);}else {
//                    这里是 cur.bf == -1,进行右左双旋rotateRL(parent);}}else {
//                这里是 parent.bf == -2if (cur.bf == -1) {
//                        这里进行右旋rotateRight(parent);}else {
//                    这里是 cur.bf == 1,进行左右双旋rotateLR(parent);}}
//                注意：只要进行过一次旋转，该树便会平衡，无需继续该 while 循环break;}}return true;}

验证 AVL 树

两条性质：

中序遍历 AVL 树可以得到一个有序序列
每个结点子树高度差的绝对值不超过 1

代码：

//    验证是否平衡public boolean isBalanced(TreeNode root) {if(root == null) {return true;}int leftH = height(root.left);int rightH = height(root.right);if(rightH - leftH != root.bf) {System.out.println("结点：" + root.val + "的平衡因子异常");return false;}return Math.abs(leftH - rightH) <= 1 &&isBalanced(root.left) &&isBalanced(root.right);}//    求树的高度private int height(TreeNode root) {if(root == null) {return 0;}int leftH = height(root.left);int rightH =height(root.right);return leftH > rightH ? leftH+1 : rightH+1;}//    验证顺序public void dfs(TreeNode root) {if (root == null) {return;}dfs(root.left);System.out.println("root = " + root.val + "; ");dfs(root.right);}

AVL 树的性能

优点:

AVL树是一颗绝对平衡的二叉搜索树，所以能够保证十分高效的查询，其时间复杂度为log2(N)

缺点：

AVL 树不适合大量的插入和删除，因为要不断的维持AVL树的平衡，从而需要进行大量的旋转

总结：

需要高效查询且有序的数据结构，且该数据不会改变，可使用 AVL 树，如果该数据经常发生变化，则不适用于 AVL 树

查看全文

http://www.15wanjia.com/news/16930.html