一、背包能否装满？

416. 分割等和子集

class Solution {
public:// 01背包：逆序遍历// 组合问题：先背包后容量bool canPartition(vector<int>& nums) {int m = nums.size();int sum = accumulate(nums.begin(), nums.end(), 0);if(sum & 1) return false;int n = sum / 2;vector<int> dp(n + 1, 0);        // dp[j]：容量为j的背包，最多装入重量为dp[j]的物品for(int i = 0; i < m; i++){for(int j = n; j >= nums[i]; j--){dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);}}return dp[n] == n;}
};

dp背包问题——416. 分割等和子集

1049. 最后一块石头的重量 II

class Solution {
public:// 01背包：逆序遍历// 组合问题：先物品、后容量int lastStoneWeightII(vector<int>& stones) {int m = stones.size();int sum = accumulate(stones.begin(), stones.end(), 0);int n = sum / 2;vector<int> dp(n + 1, 0);  // dp[j]：容量为j的背包，最多装dp[j]的石头for(int i = 0; i < m; i++){for(int j = n; j >= stones[i]; j--){dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - 2 * dp[n];}
};

dp背包问题——1049. 最后一块石头的重量 II

二、装满背包有几种方法？

494. 目标和

class Solution {
public:// 01背包：逆序遍历// 组合问题：先物品，后容量int findTargetSumWays(vector<int>& nums, int target) {int sum = accumulate(nums.begin(), nums.end(), 0);if((sum + target) & 1) return 0;int m = nums.size();int n = (sum + target) / 2;if(n < 0) return 0;vector<int> dp(n + 1, 0);  // dp[j]：装满容量为j的背包，有dp[j]种方法dp[0] = 1;                 // 装满容量为0的背包，只有1种方法for(int i = 0; i < m; i++){for(int j = n; j >= nums[i]; j--){// 多了一个物品可选择后，装满背包的方法数就是 ：（没有当前物品可选时的方法数 + 选了当前物品的方法数）dp[j] = dp[j] + dp[j - nums[i]];}}return dp[n];}
};

dp背包解决组合问题——494. 目标和

518.零钱兑换II

class Solution {
public:// 完全背包：顺序遍历// 组合问题：先物品、后容量int change(int amount, vector<int>& coins) {int m = coins.size();int n = amount;vector<int> dp(n + 1, 0);  // dp[j]：装满容量为j的背包，有dp[j]种方式dp[0] = 1;for(int i = 0; i < m; i++){for(int j = coins[i]; j <= n; j++){// 多了一个物品可选后，装满背包的方法数就是 ：（没有当前物品可选时的方法数 + 选了当前物品的方法数）dp[j] = dp[j] + dp[j - coins[i]];}}return dp[n];}
};

dp完全背包问题解组合问题——零钱兑换

377. 组合总和 Ⅳ

class Solution {
public:// 完全背包：顺序遍历// 排列问题：先容量，后物品int combinationSum4(vector<int>& nums, int target) {int m = nums.size();int n = target;vector<int> dp(n + 1, 0); // dp[j]：装满容量为j的背包，物品的组合数为dp[j]dp[0] = 1;for(int j = 1; j <= n; j++){for(int i = 0; i < m; i++){if(j >= nums[i] && dp[j] < INT_MAX - dp[j - nums[i]]) dp[j] += dp[j - nums[i]];}}return dp[n];}
};

70. 爬楼梯

class Solution {
public:// 完全背包：顺序遍历// 排列问题：先容量，后物品int climbStairs(int n) {int m = 2;int nums[2] = {1,2};vector<int> dp(n + 1, 0);  // dp[j]：装满容量为j的背包，有dp[j]种方法dp[0] = 1;for(int j = 1; j <= n; j++){for(int i = 0; i < m; i++){if(j >= nums[i]) dp[j] = dp[j] + dp[j - nums[i]];}}return dp[n];}
};

排列问题：先容量，后物品

如果物品为{1，2}，假如此时容量为2（容量为1的背包只能装物品1），用当前容量遍历多个物品，可以选择在装了物品1的基础上接着装，也可以选择不在其基础上装，直接装入物品2。当容量为3时，也可以选择在装有物品2的基础上再装入物品1，这样就出现了{2，1}

组合问题：先物品，后容量

如果物品为{1，2，3}，假如此时容量为5

只有物品1，用各个容量遍历，此时无论是什么容量的背包，都只能放入物品1
此时我们手拿着物品2，对于每一个容量，要么直接使用现在就装满的背包，要么找一个剩余容量为2的背包放入当前物品2
接着我们手拿着物品3，对于每一个容量，要么直接使用现在就装满的背包，要么找一个剩余容量为3的背包放入当前物品3

class Solution {
public:int climbStairs(int n) {vector<int> dp(n + 1, 0);dp[0] = 1;dp[1] = 1;for(int i = 2; i <= n; i++){dp[i] = dp[i - 2] + dp[i - 1];  // 要么爬1个台阶，要么2个台阶}return dp[n];}
};

三、背包装满的最大价值

474.一和零

class Solution {
public:// 01背包：逆序遍历// 组合问题：先物品、后容量int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));  // dp[i][j]：装满容量为ij背包的最大价值for(string& s : strs){int w0 = 0;int w1 = 0;for(char c : s){if(c == '0') w0++;else w1++;}// 每次循环计算出的dp[m][n]表示只有前几个物品可选时，所获得的最大价值for(int i = m; i >= w0; i--){for(int j = n; j >= w1; j--){dp[i][j] = max(dp[i][j], dp[i - w0][j - w1] + 1);  // 1表示价值}}}return dp[m][n];}
};

四、装满背包最小物品数

322. 零钱兑换

class Solution {
public:// 问装满背包需要最少的物品数int coinChange(vector<int>& coins, int amount) {// 完全背包：顺序遍历// 组合问题：先物品、后容量，装满就行，不在意装入的顺序int m = coins.size();int n = amount;// 凑成面值n，最多需要n个硬币，初始化为n + 1即可vector<int> dp(n + 1, n + 1); // dp[j]：装满容量为j的背包至少需要dp[j]个物品dp[0] = 0;for(int i = 0; i < m; i++){for(int j = coins[i]; j <= n; j++){// 装满容量为j的背包，要么直接用前面的物品装满，要么找一个剩余容量为coins[i]的背包放入coins[i]dp[j] = min(dp[j], dp[j - coins[i]] + 1);  }}return dp[n] == n + 1 ? -1 : dp[n];}
};

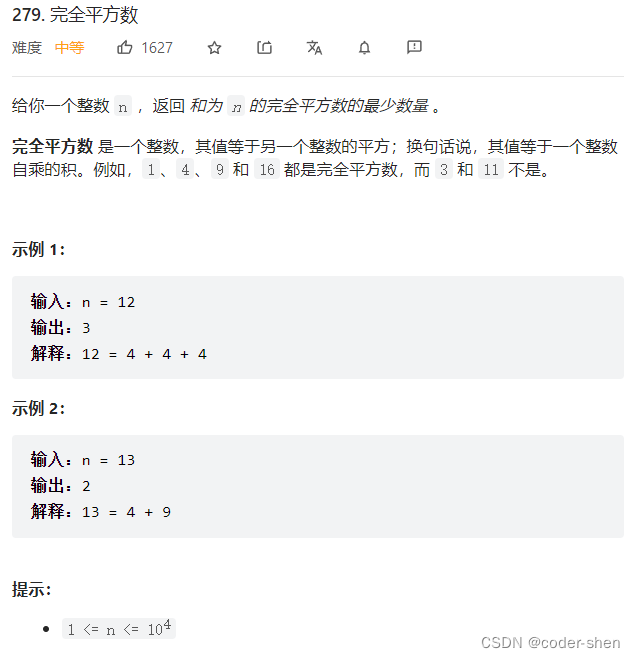
279.完全平方数

class Solution {
public:// 物品为：[1,4,9,...]// 容量为n，问装满背包至少需要几个物品int numSquares(int n) {// 完全背包：顺序遍历// 组合问题：先物品、后容量vector<int> dp(n + 1, n);dp[0] = 0;for(int i = 1; i <= n / i; i++){for(int j = i * i; j <= n; j++){dp[j] = min(dp[j], dp[j - i * i] + 1);}}return dp[n];}
};