"相信羁绊，相信微光，相信一切无常。"

一、AVL树翻转那些事儿

(1)什么是AVL树？

在计算机科学中，AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。而保证这颗树平衡的关键步骤，就是通过旋转来保证，由于增加、删除时对树的破坏的平衡。 取自这里

这样的树形结构，能够十分高效地查找"键值"(key/value模型)。C++中的STL容器，如map、set其底层就是由红黑树实现的。当然这是后半段会讲的一种优秀的数据结构。

AVL规则:
它的左右子树都是AVL树。
左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)。

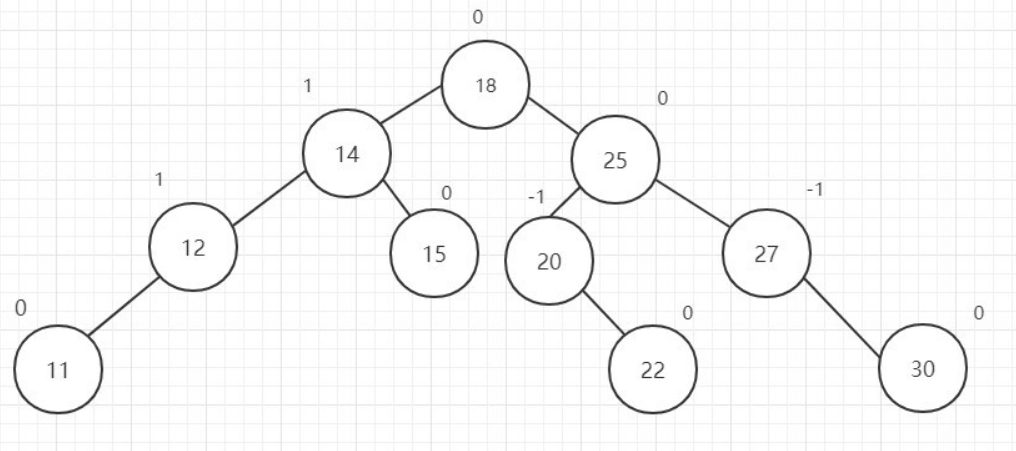
形如上图，每个节点的上标是该节点的左右子树的高度差。如果该AVL二叉树有N个节点,那么其高度可以保持LogN(以2为底)，其搜索查找的时间复杂度为LogN(以2为底)。

(2)翻转那些事儿

条件检测;

上面的简介也说过，AVL树的平衡是通过旋转来维护的。那么什么时候需要翻转呢？什么时候不需要呢？我们在这里对每个节点引入 "平衡因子(bf)"的概念。对节点左右子树高度的检测，转移到了对平衡因子数值状态的检测。

root(当前节点) 我们对插入节点对平衡因子的更改做一个约定:左插入-- 右插入++。
① bf == 0时,说明当前左右子树高度平衡，不需要调整。
② bf == 1 || bf == -1时,说明这颗"root一定是从bf == 0变化而来的"。那么就不仅仅需要关注当前root节点平衡因子的变化,还需要"向上调整"。root = root->parent
③ bf == 2 || bf == -2 时,此时AVL条件树的已经不平衡了 需要手动翻转才能保证其平衡性。

单线旋转;

节点属性:

template<class K,class V>
struct AVLTreeNode
{std::pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;int _bf = 0;AVLTreeNode(const std::pair<K,V> kv):_kv(kv),_left(nullptr),_right(nullptr),_bf(0){}
};

RotateR:

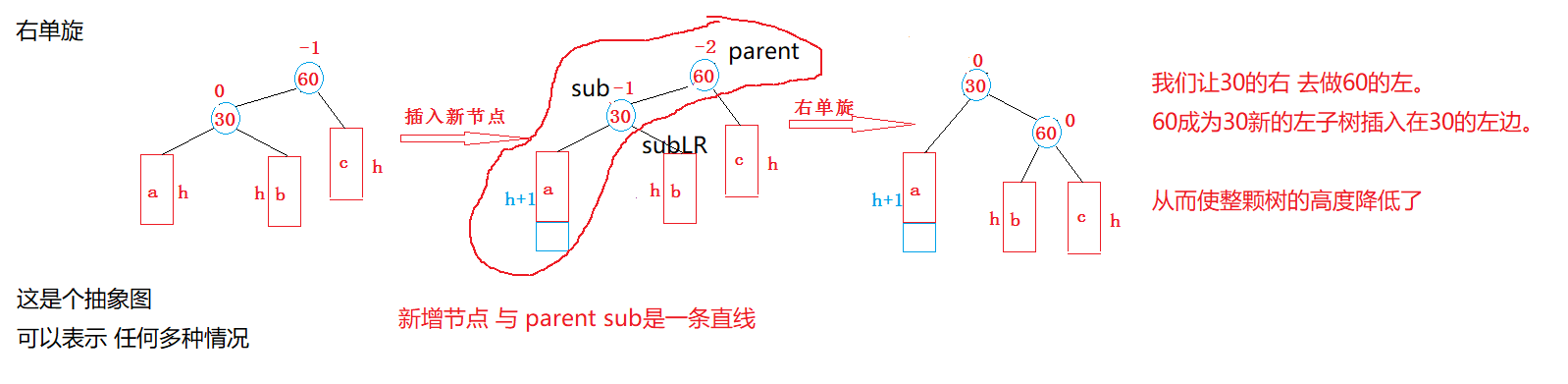
①让subLR作为左子树 连接在parent的左边。
②parent再作为subL的右子树连接。
③subL成为新的当前左右子树的根，并与上层parent->parent连接

void RotateL(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){//subLR 如果不为空才需要 连接parentsubLR->_parent = parent;}//连接诶父节点Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (root == nullptr){subL = root;subL->_parent == nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}//更新平衡因子subL->_bf = parent->_bf = 0;
}

RotateL:

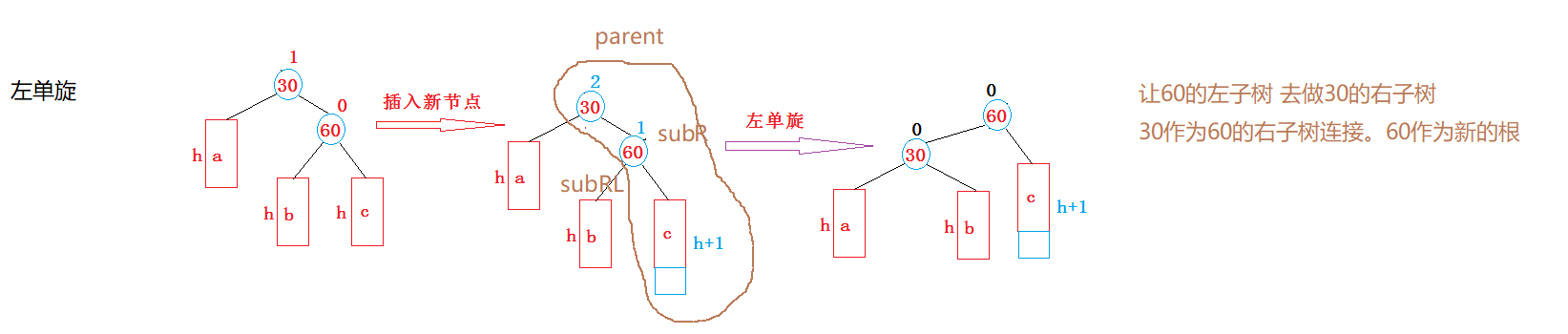
①让subRL作为30的右子树连接。
②parent作为subR的左子树连接。
③subR作为新的当前左右子树的根，并与上层parent->parent连接。

void RotateR(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;parent->_parent = subR;subR->_right = parent;if (root== nullptr){root = subR;subR->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}subR->_bf = parent->_bf = 0;
}

折线旋转;

其实单线旋转蛮简单的，并且旋转过后平衡因子都可以被直接处理为0。但是，如果是面对折线旋转的情况，仅仅考单旋处理，是不够的。

左右双旋:

右左双旋:

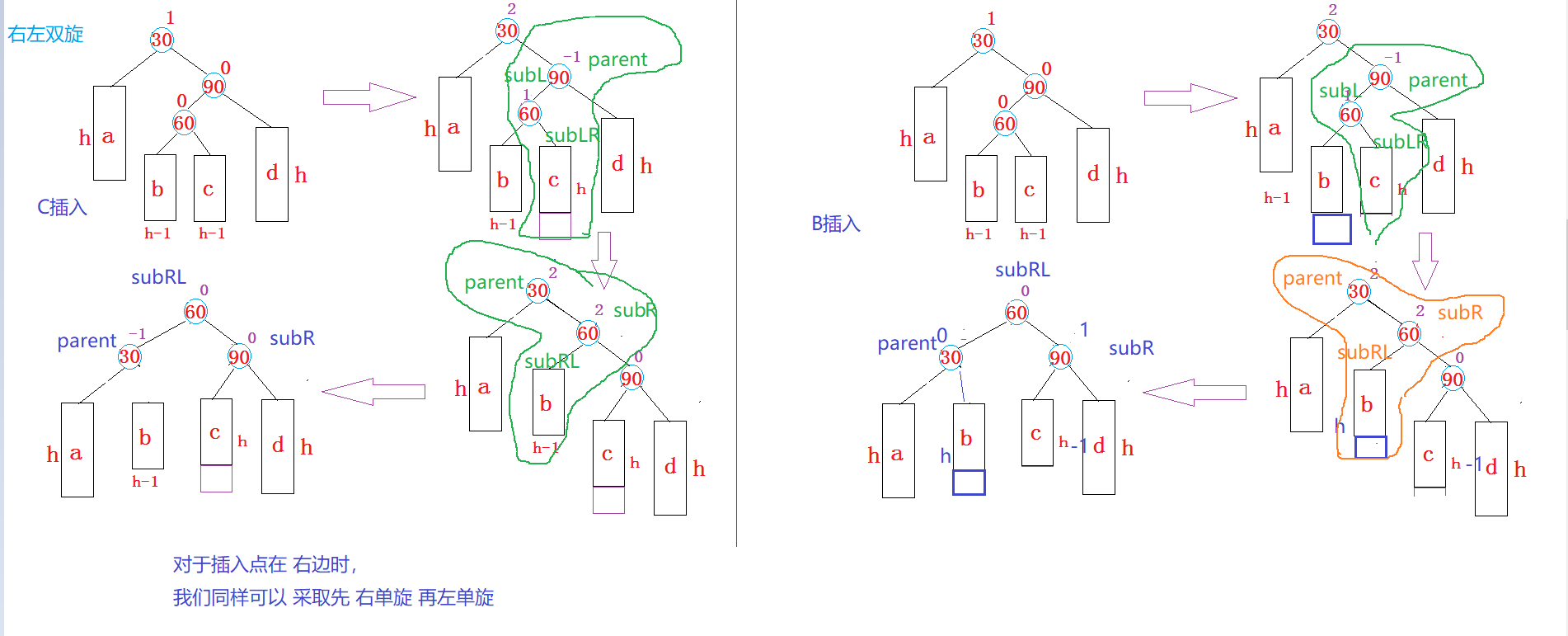
双旋的问题，我觉得难点不是在于旋转，因为前面已经解决了。而是如何处理双旋后的平衡因子与什么时候用双旋，什么时候用单旋？

单旋的判断很简单，因为是一条直线
即: (parent->bf == 2 && cur->bf == 1) || (parent->bf == -2 && cur->bf == -1)

双旋使用的场景，就是针对折线的插入节点
即: (parent->bf == 2 && cur->bf == -1) || (parent->bf == -2 && cur->bf == 1)

单旋情况下平衡因子的处理颇为简单易懂，一次翻转就可以将左右子树高度调平。

双旋情况下的平衡因子取决于subRL \ subLR 到底是左子树+1 还是右子树+1
对于右左双旋的情况,subRL的左子树会被parent去接手，反之subRL的右子树会被subL接手。

对于左右双旋的情况,subLR的左子树会被subR接手，而它的右子树会被parent接手。
其实还是一句话，画图才是王道。

void RotateRL(Node* parent)
{Node* subL = parent->_right;Node* subLR = subL->_left;//依据int bf = subLR->_bf;RotateR(subL);RotateL(parent);//说明是在cur的 左边插入if (bf == -1){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}else if (bf == 1){//说明是在cur的 右边插入subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}else{subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}
}void RotateLR(Node* parent)
{Node* subR = parent->_right;Node* subRL = parent->_left;int bf = subRL->_bf;RotateL(subR);RotateR(parent);if (bf == -1){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else{subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}
}

二、红黑树翻转那些事儿

(1)什么是红黑树?

红黑树（Red Black Tree） 是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。

为什么有了AVL树，又来了个红黑树呢？那必定红黑树一定有比起AVL树更加优势的地方。可以说,"AVL树是一位大佬设想,那么红黑树一定是出自一位天才的手笔。"

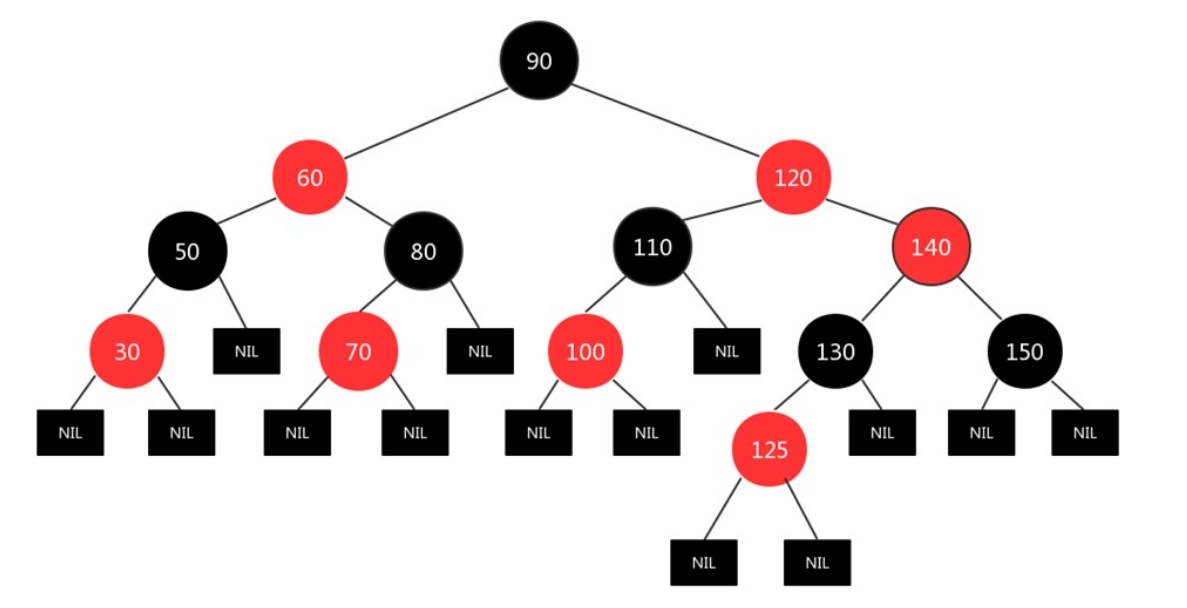
红黑树规则:
①每个结点不是红色就是黑色。
②根节点一定是黑色。
③不能出现连续的红色结点。
④对于每个结点到后代结点的简单路径上，都含有相同的黑色结点。

红黑树没有像AVL树那么严格地控制平衡(左右子树高度差不超过1)，它是一种接近平衡的搜索二叉树。

红黑树规则的核心: 确保最长路径的结点数不超过最短路径节点数的2倍。

(2)翻转那些事儿

条件检测:

红黑树插入结点的情况，其实可以分为两大类:

①cur(新增结点)红 parent红 grandparent黑 uncle红

②cur(新增结点)红 paren红 grandparent黑 uncle不存在或者存在且为黑。

由此红黑树插入的关键为：uncle结点。

下面来看看这两种情况的对应图:

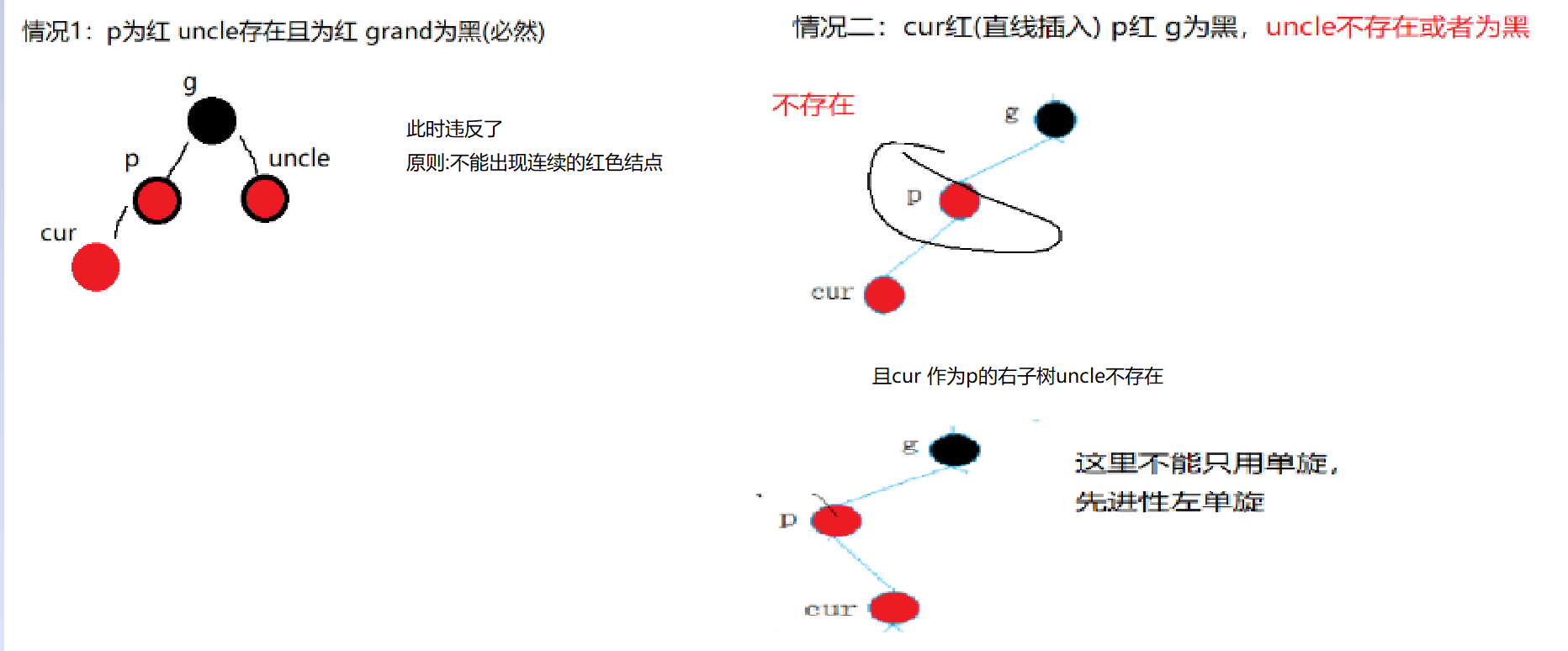
因为牵涉到翻转，正好我们也在AVL树那一小结写过，直接CV一份~

void RotateL(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (ppNode->_parent == nullptr){subL = root;subL->_parent == nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}
}void RotateR(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;parent->_parent = subR;subR->_right = parent;if (root== nullptr){root = subR;subR->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}

红黑树结点结构;

enum Color
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{std::pair<K, V> _kv;RBTreeNode<K, V>* _left = nullptr;RBTreeNode<K, V>* _right = nullptr;RBTreeNode<K, V>* _parent = nullptr;Color _color = RED;RBTreeNode(const std::pair<K, V>& kv):_kv(kv){}
};

uncle存在且为红:

我们让 parent 与 uncle同时变黑 并且 grandparent变为红色。

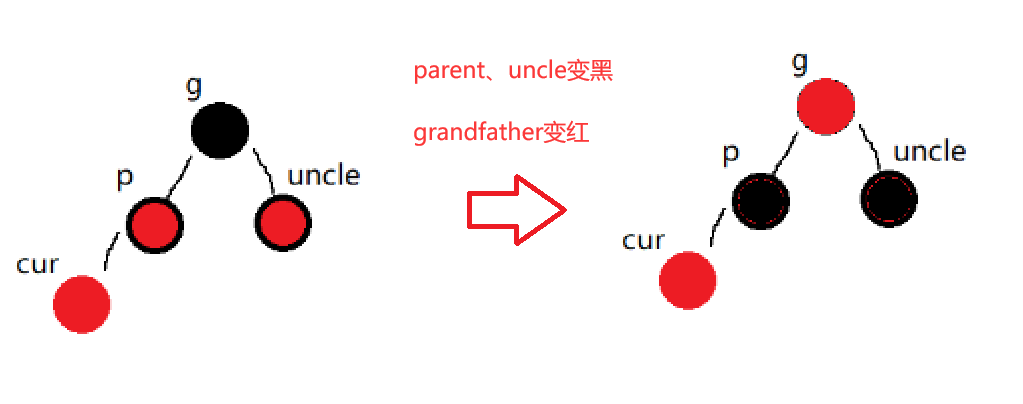
就结束了吗？当然不是！

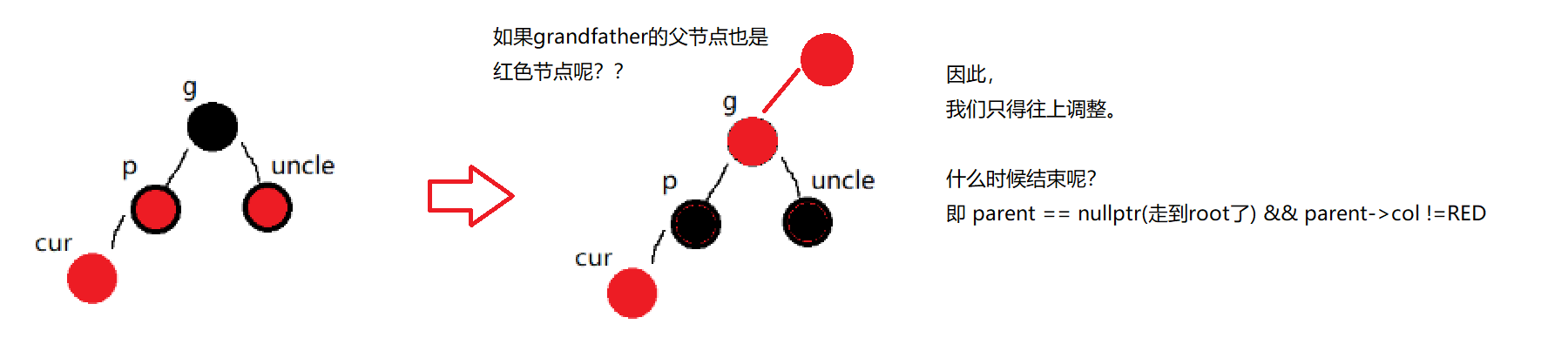
bool Insert(const std::pair<K,V>& kv)
{//..Node* cur = new Node(kv);Node* parent = cur->_parent;while (parent &&parent->_color!= RED){Node* grandfather = parent->_parent;//找到uncle节点Node* uncle = nullptr;if (grandfather->_left == parent){uncle = grandfather->_right;//1.uncle存在且为红if (uncle && uncle->_color == RED){//着色uncle->_color = parent->_color = BLACK;grandfather->_color = RED;//继续向上调整cur = grandfather;parent = cur->_parent;}//......}else{uncle = grandfather->_left;//1.uncle存在且为红if (uncle && uncle->_color == RED){//着色uncle->_color = parent->_color = BLACK;grandfather->_color = RED;//继续调整cur = grandfather;parent = cur->_parent;}//......}}}

uncle不存在或者uncle存在且为黑(cur为直线):

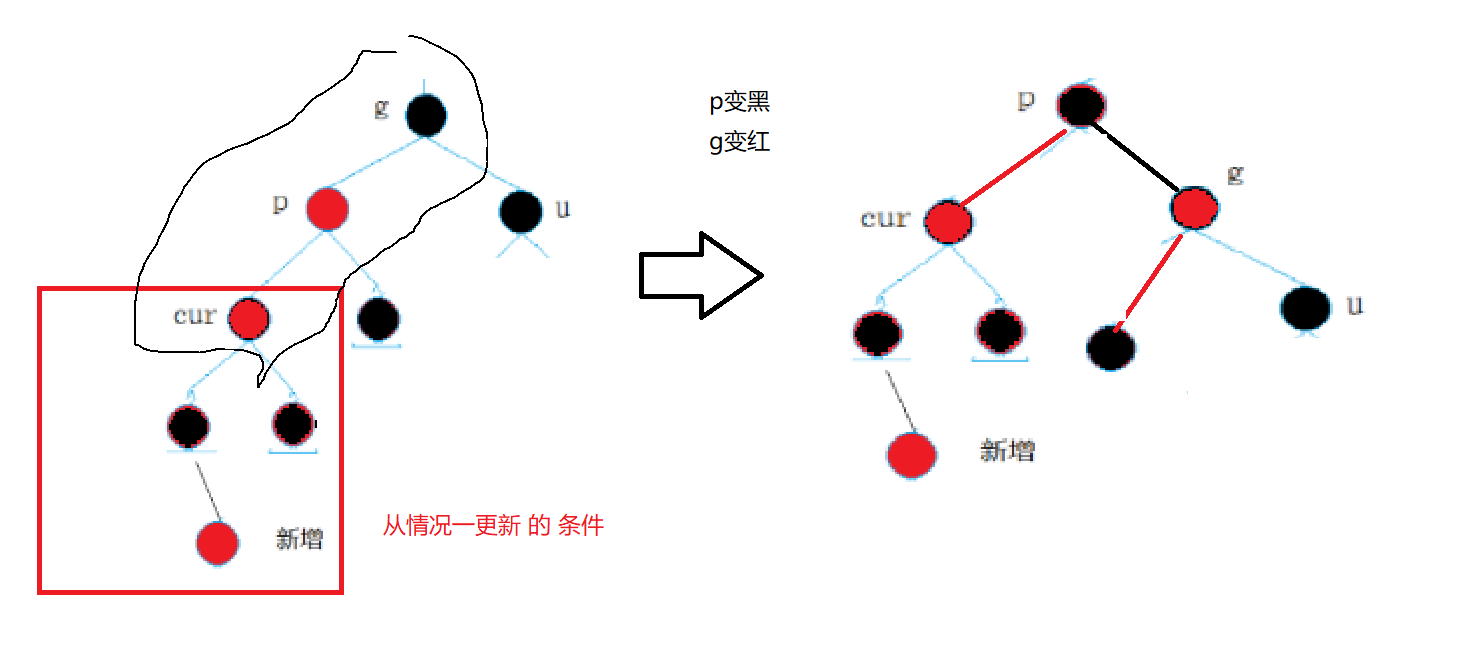
我们让parent变黑 grandfather变红

//uncle = grandfather->_right;
//uncle不存在或者存在且为黑
//parent在左  uncle在右  左子树
if (cur == parent->_left)
{RotateR(grandfather);//着色grandfather->_color = RED;parent->_color = BLACK;
}//uncle = grandfather->_left;
//uncle不存在或者存在且为黑
//parent在右  uncle在左 右子树
if (cur == parent->_right)
{RotateL(grandfather);grandfather->_color = RED;parent->_color = BLACK;
}

uncle不存在或者uncle存在且为黑色(折线)

进一步复杂的情况，不单单是用单旋搞定。

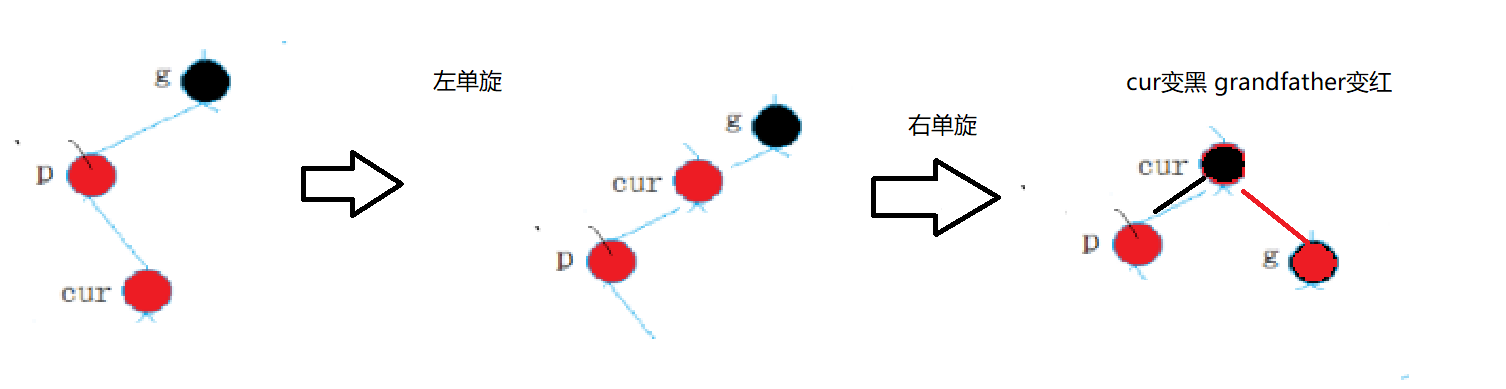
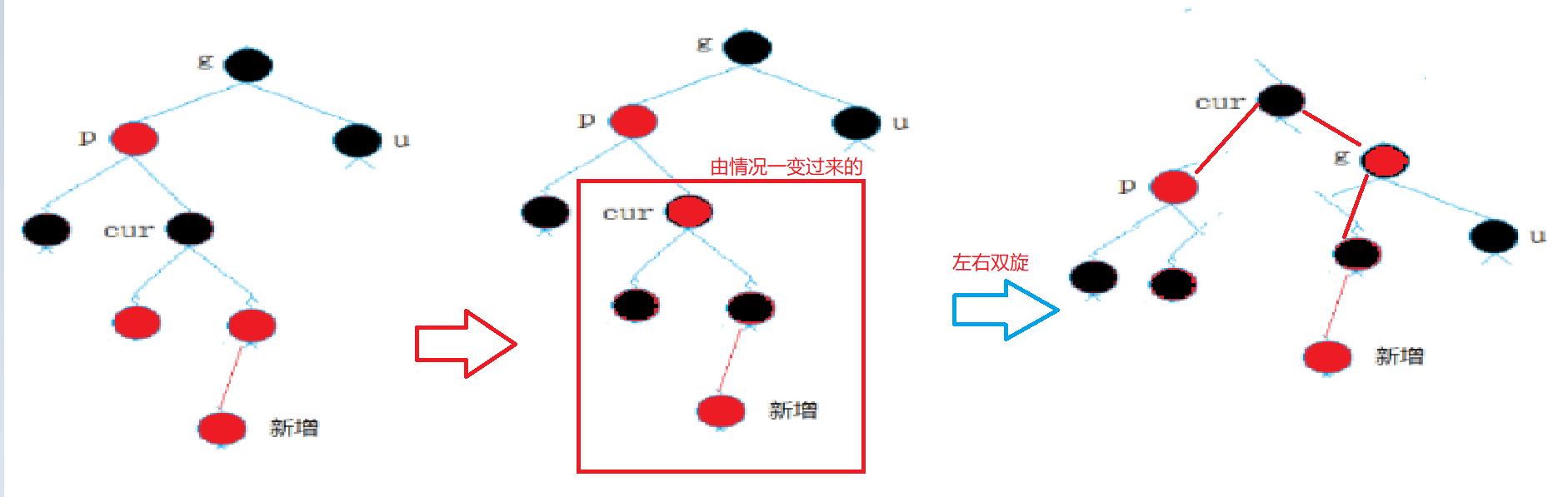
我们将cur变黑，grandfather变红

//uncle = grandfather->_right;
else{RotateL(parent);RotateR(grandfather);grandfather->_color = RED;cur->_color = BLACK;
}
//uncle = grandfather->_left;
//cur == parent->_left
else{RotateR(parent);RotateL(grandfather);grandfather->_color = RED;cur->_color = BLACK;
}

总结:

AVL与红黑树都是搜索效率极其强悍的数据结构。红黑树不追求绝对的平衡，但是AVL却对左右子树的平衡关系严格要求。因此，对树的翻转次数一定多余红黑树。在插入时其性能效率也会相应受到影响。而且红黑树实现比较简单，所以实际运用中红黑树更多。

本篇到此为止，感谢你的阅读。

祝你好运，向阳而生~